题目内容
12.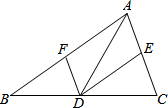 如图,△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,则
如图,△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,则①如果∠BAC=90°,那么四边形AEDF是矩形;
②如果AD平分∠BAC,那么四边形AEDF是菱形;
③如果AD⊥BC且AB=BC,那么四边形AEDF是菱形.
以上说法正确的有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 都不正确 |
分析 先由两组对边分别平行的四边形为平行四边形,根据DE∥CA,DF∥BA,得出AEDF为平行四边形,当∠BAC=90°,根据推出的平行四边形AEDF,利用有一个角为直角的平行四边形为矩形可得出①正确;
若AD平分∠BAC,得到一对角相等,再根据两直线平行内错角相等又得到一对角相等,等量代换可得∠EAD=∠EDA,利用等角对等边可得一组邻边相等,根据邻边相等的平行四边形为菱形可得出②正确;
当AD⊥BC且AB=BC,不能得出四边形AEDF是菱形,③不一定正确;即可得出结论.
解答 解:①正确;理由如下:
∵DE∥CA,DF∥BA,
∴四边形AEDF是平行四边形,
当∠BAC=90°时,四边形AEDF是矩形(有一个角是直角的平行四边形是矩形);
②正确;理由如下:
∵DE∥CA,DF∥BA,
∴四边形AEDF是平行四边形,∠BAD=∠EDA,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
∴∠EDA=∠EAD,
∴AE=DE,
∴四边形AEDF是菱形(有一组邻边相等的平行四边形是菱形);
③不一定正确;
∵AD⊥BC且AB=BC,不能得出四边形AEDF是菱形,
∴③不一定正确;
正确的说法由2个,
故选:B.
点评 此题考查了平行四边形的判定、矩形的判定、菱形的判定;熟练掌握平行四边形和矩形、菱形的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
7.小颖为了解家里的用电量,在4月初同一时刻观察家里电表显示的数字,记录如下:
估计小颖家4月份的总用电量是120千瓦时.
| 日期(号) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 电表显示的数字(千瓦时) | 117 | 120 | 124 | 129 | 135 | 138 | 142 | 145 |
4.下列运算中结果正确的是( )
| A. | 3a+2b=5ab | B. | 5y-3y=2 | C. | -3x+5x=-8x | D. | 2x2y-3x2y=-x2y |
 已知△ABC和一点O,以点O为位似中心,作△DEF,使它与△ABC位似,且相似比是2:1.
已知△ABC和一点O,以点O为位似中心,作△DEF,使它与△ABC位似,且相似比是2:1. 如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P从点A出发,以3cm/s的速度向点B为止;动点Q同时从点C出发,以2cm/s的速度向点D运动.何时点P和Q之间的距离是10cm?
如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P从点A出发,以3cm/s的速度向点B为止;动点Q同时从点C出发,以2cm/s的速度向点D运动.何时点P和Q之间的距离是10cm?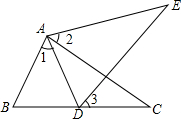 如图,点D在BC上,∠1=∠2=∠3,DE=BC,求证:AE=AC.
如图,点D在BC上,∠1=∠2=∠3,DE=BC,求证:AE=AC.