题目内容

20．已知：A=a+a1+a2+a3+…+a2014，若a=-1，则A=-1．

分析 根据有理数的乘方，即可解答．

解答 解：若a=-1，
则A=（-1）+（-1）1+（-1）2+（-1）3+…+（-1）2014
=-1+（-1）+1+（-1）+…+1
=-1．
故答案为：-1．

点评 本题考查了有理数的乘方，解决本题的根据是熟记有理数的乘方．

练习册系列答案
相关题目
10．下列方程是关于x的一元二次方程的是（　　）
A．x2+2y+1=0B．$\frac{1}{x^2}+\frac{1}{x}$=2C．ax2+bx+c=0D．3（x+1）2=2（x+1）
11．用配方法解方程x2-4x-6=0时，下列变形正确的是（　　）
A．（x-2）2=6B．（x-2）2=10C．（x-4）2=6D．（x-4）2=10
8．已知2011x2014+2012x2013+2013x2012+2014=1021x2014+1022x2013+1023x2012-956，那么x2014+x2013+x2012-1的值为（　　）
A．-44B．-34C．-24D．-14
15．用代数式表示图中阴影部分的面积，并计算当a=10，b=3.5时的面积．
5．如果方程x2+bx+c=0的两个根分别是2和-5，那么2b-c=16．
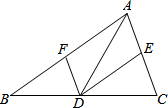12．如图，△ABC中，点D、E、F分别在边BC、AB、CA上，且DE∥CA，DF∥BA，则
①如果∠BAC=90°，那么四边形AEDF是矩形；
②如果AD平分∠BAC，那么四边形AEDF是菱形；
③如果AD⊥BC且AB=BC，那么四边形AEDF是菱形．
以上说法正确的有（　　）
A．3个B．2个C．1个D．都不正确
9．书店卖课本和笔记本，课本每本定价20元，笔记本每本定价2元．书店开展促销活动，向客户提供两种优惠方案：①买一本课本送一本笔记本；②课本和笔记本都按定价的95%付款．现某班要到该书店购买课本50本，笔记本x本（x＞50）．（用含x的代数式表示）
（1）若该客户按方案①购买，需付款多少元？
（2）若该客户按方案②购买，需付款多少元？
（3）若x=300，通过计算说明此时按哪种方案购买较为合算？
10．将连续正整数1，2，3，4…按如图的规律排列，则数字2014在第12行，第45列．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网