题目内容
2.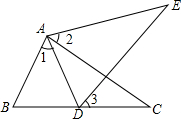 如图,点D在BC上,∠1=∠2=∠3,DE=BC,求证:AE=AC.
如图,点D在BC上,∠1=∠2=∠3,DE=BC,求证:AE=AC.
分析 如图所示由∠2=∠3,∠4=∠5可知:∠E=∠C,然后再证明∠BAC=∠DAE,最后利用AAS证明△BAC≌△DAE,从而可得到AE=AC.
解答 解:如图所示:
∵∠2=∠3,∠4=∠5,
∴∠E=∠C.
∵∠2=∠1,
∴∠BAC=∠DAE.
在△BAC和△DAE中,$\left\{\begin{array}{l}{∠E=∠C}\\{∠BAC=∠DAE}\\{DE=BC}\end{array}\right.$,
∴△BAC≌△DAE.
∴AE=AC.
点评 本题主要考查的是全等三角形的性质和判定、三角形的内角和定理的应用,证得∠E=∠C是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
12.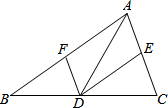 如图,△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,则
如图,△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,则
①如果∠BAC=90°,那么四边形AEDF是矩形;
②如果AD平分∠BAC,那么四边形AEDF是菱形;
③如果AD⊥BC且AB=BC,那么四边形AEDF是菱形.
以上说法正确的有( )
 如图,△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,则
如图,△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA,则①如果∠BAC=90°,那么四边形AEDF是矩形;
②如果AD平分∠BAC,那么四边形AEDF是菱形;
③如果AD⊥BC且AB=BC,那么四边形AEDF是菱形.
以上说法正确的有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 都不正确 |
14.关于a+b+c=0,则关于x的方程ax2+bx+c=0(a≠0)必有一根为( )
| A. | x=0 | B. | x=-1 | C. | x=1 | D. | x=2 |
 将连续正整数1,2,3,4…按如图的规律排列,则数字2014在第12行,第45列.
将连续正整数1,2,3,4…按如图的规律排列,则数字2014在第12行,第45列.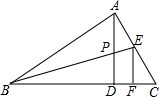 如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,P是AD的中点,BP交AC于点E,EF⊥BC于点F,若AE=3,EC=4,求EF的值.
如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,P是AD的中点,BP交AC于点E,EF⊥BC于点F,若AE=3,EC=4,求EF的值.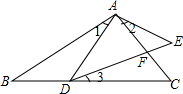 如图,∠1=∠2=∠3.试说明:AB•AE=AD•AC.
如图,∠1=∠2=∠3.试说明:AB•AE=AD•AC.