Question

2．在锐角三角形ABC中，BD⊥AC于D，CE⊥AB于E，且S_△ADE=$\frac{1}{3}$S_{四边形BEDC}，则∠A=（　　）

• A． 75°
• B． 60°
• C． 45°
• D． 30°

Answer 1

分析 如图，连接DE，首先证明△AED∽△ACB，根据相似三角形的性质，推出AC=2AE，由sin∠ACE=$\frac{AE}{AC}$=$\frac{1}{2}$，求出∠ACE即可解决问题．

解答 解：如图，连接DE．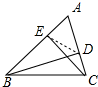

∵BD⊥AC于D，CE⊥AB于E，
∴∠AEC=∠ADB=90°，
∵∠A=∠A，
∴△ABD∽△ACE，
∴$\frac{AB}{AC}$=$\frac{AD}{AE}$，
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$，∵∠A=∠A，
∴△AED∽△ACB，
∵S_△ADE=$\frac{1}{3}$S_{四边形BEDC}
∴S_△ADE：S_△ABC=1：4
∴（$\frac{AE}{AC}$）²=$\frac{1}{4}$，
∴AC=2AE，
∴sin∠ACE=$\frac{AE}{AC}$=$\frac{1}{2}$，
∴∠ACE=30°，
∴∠A=90°-∠ACE=60°，
故选B．

点评 本题考查相似三角形的性质和判定、解题的关键是利用相似三角形的性质，相似三角形的面积比等于相似比的平方，属于中考常考题型．