题目内容
5.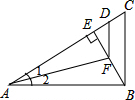 如图,已知:AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则①BF=DF,②DF=BC,③∠ADF=∠C=∠ABE,④FD∥BC,⑤∠CAB=∠CBE=∠DFE,其中正确①④⑤(只填序号).
如图,已知:AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则①BF=DF,②DF=BC,③∠ADF=∠C=∠ABE,④FD∥BC,⑤∠CAB=∠CBE=∠DFE,其中正确①④⑤(只填序号).
分析 根据题中的条件可证明出△ADF≌△ABF,由全等三角形的性质可的∠ADF=∠ABF,再由条件证明出∠ABF=∠C,由角的传递性可得∠ADF=∠C,根据平行线的判定定理可证出FD∥BC.
解答 解:在△AFD和△AFB中,
∵AF=AF,∠1=∠2,AD=AB,
∴△ADF≌△ABF,
∴∠ADF=∠ABF,BF=DF.
∴①正确,②错误;
∵AB⊥BC,BE⊥AC,
即:∠BAC+∠C=∠BAC+∠ABF=90°,
∴∠ABF=∠C,
即:∠ADF=∠ABF=∠C,
∴③错误;
∴FD∥BC,④正确
⑤∠CAB=∠CBE=∠DFE,正确;
故答案为:①④⑤
点评 本题主要考查全等三角形的性质,涉及到的知识点还有平行线的判定定理,关键在于运用全等三角形的性质证明出角与角之间的关系.

练习册系列答案
相关题目
13.将一些完全相同的棋子按如图所示的规律摆放,第1个图形有4颗棋子,第2个图形有13颗棋子,第3个图形有28颗棋子,…,按此规律,则第6个图形中共有棋子的颗数是( )


| A. | 107 | B. | 109 | C. | 112 | D. | 115 |
14.若3x=4,9y=7,则3x+2y的值为( )
| A. | 28 | B. | 3 | C. | 11 | D. | 47 |
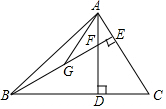 如图,△ABC中,∠ABC=45°,高AD和BE交于F点,点G为BF的中点,AF=4,DF=6,则AG=$\frac{10\sqrt{170}}{17}$.
如图,△ABC中,∠ABC=45°,高AD和BE交于F点,点G为BF的中点,AF=4,DF=6,则AG=$\frac{10\sqrt{170}}{17}$. 如图,AB=AD=4cm,BC=CD,若∠ABD=60°,则BE=2cm.
如图,AB=AD=4cm,BC=CD,若∠ABD=60°,则BE=2cm.