题目内容
3.将一根长为16cm的铁丝首尾相接围成一个扇形,求这个扇形面积的最大值.分析 设这个扇形半径为xcm,扇形面积为S,首先表示出扇形的弧长为(16-2x)cm,进而利用S扇形=$\frac{1}{2}$lr列出函数解析式,利用配方法求得最大值即可.
解答 解:设这个扇形半径为xcm,扇形面积为S,由题意得
S=$\frac{1}{2}$x(16-2x)
=-x2+8x
=-(x-4)2+16.
故这个扇形面积的最大值是16cm2.
点评 此题考查二次函数的实际运用,利用扇形面积公式得出解析式是解题关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
13.如图是一个立体图的主视图左视图和俯视图(图中单位为厘米),则立体图形的体积为多少?( )
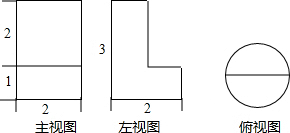

| A. | π | B. | 2π | C. | 3π | D. | 4π |
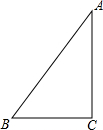 某年某地地震造成了大量的山体滑坡,其中有一处长为60米的滑坡覆盖了整条公路,使原来平坦的公路成了与山坡浑然一体的斜坡,如图的直角三角形ABC是塌方的横截面,为了及时清除这路段上的塌方,必须马上估计塌方的数量.工程兵测得原来公路的宽BC=12米,坡角∠ABC=60°,如果采用一台每小时可清除100立方米的挖掘机,全部清理完这个路段需要多少小时?(精确到1小时)
某年某地地震造成了大量的山体滑坡,其中有一处长为60米的滑坡覆盖了整条公路,使原来平坦的公路成了与山坡浑然一体的斜坡,如图的直角三角形ABC是塌方的横截面,为了及时清除这路段上的塌方,必须马上估计塌方的数量.工程兵测得原来公路的宽BC=12米,坡角∠ABC=60°,如果采用一台每小时可清除100立方米的挖掘机,全部清理完这个路段需要多少小时?(精确到1小时)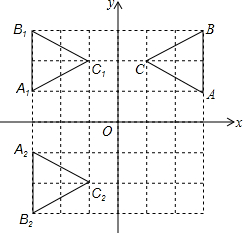 如图,在平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以y轴为对称轴作△ABC的对称图形得△A1B1C1,再以x轴为对称轴作的对称图形,得△A2B2C2.
如图,在平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以y轴为对称轴作△ABC的对称图形得△A1B1C1,再以x轴为对称轴作的对称图形,得△A2B2C2.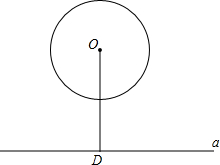 如图,⊙O的半径为3cm,OD垂直于直线a,垂足为D,OD=4cm,问直线a向上平移几厘米时,直线a与⊙O有一个公共点?
如图,⊙O的半径为3cm,OD垂直于直线a,垂足为D,OD=4cm,问直线a向上平移几厘米时,直线a与⊙O有一个公共点?