题目内容
光年是天文学中的距离单位,1光年大约是9500 000 000 000km,这个数据用科学计数法表示是( )
A. 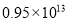 km B.
km B. 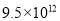 km C.
km C. 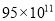 km D.
km D. 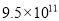 km
km
练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
题目内容
光年是天文学中的距离单位,1光年大约是9500 000 000 000km,这个数据用科学计数法表示是( )
A. 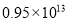 km B.
km B. 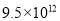 km C.
km C. 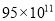 km D.
km D. 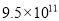 km
km
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案