题目内容
18.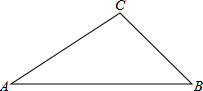 如图,在△ABC中,已知:∠A=30°,∠C=105°,AC=4,求AB和BC的长.
如图,在△ABC中,已知:∠A=30°,∠C=105°,AC=4,求AB和BC的长.
分析 过C作CD⊥AB于D,则∠CDA=∠CDB=90°,在Rt△ACD中,由∠A=30°,AC=4,求得CD=AC•sinA=2,AD=AC,cosA=2$\sqrt{3}$,根据三角形的内角和得到∠B=45°,在Rt△BCD中,根据BD=CD=2,BC=2$\sqrt{2}$,即可得到AB=2$\sqrt{3}$+2.
解答 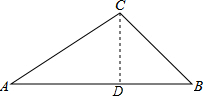 解:过C作CD⊥AB于D,则∠CDA=∠CDB=90°,
解:过C作CD⊥AB于D,则∠CDA=∠CDB=90°,
在Rt△ACD中,
∵∠A=30°,AC=4,
∴CD=AC•sinA=2,AD=AC,cosA=2$\sqrt{3}$,
∵∠A=30°,∠ACB=105°,
∴∠B=45°,
在Rt△BCD中,BD=CD=2,BC=2$\sqrt{2}$,
∴AB=2$\sqrt{3}$+2.
点评 本题考查了解直角三角形.要熟练掌握好边角之间的关系是解题的关键.

练习册系列答案
相关题目
8.若a+b+c=0,则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|abc|}{abc}$可能的值的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13. 如图,两个同心圆的半径分别为3cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的半径分别为3cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
 如图,两个同心圆的半径分别为3cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的半径分别为3cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )| A. | 3cm | B. | 4cm | C. | 6cm | D. | 8cm |
 数a在数轴上的位置如图所示,式子|a-1|-|a|的化简结果是1.
数a在数轴上的位置如图所示,式子|a-1|-|a|的化简结果是1. 如图,△ABC为等边三角形,A、B、C、D四点均在⊙O上,则∠BDC=60°.
如图,△ABC为等边三角形,A、B、C、D四点均在⊙O上,则∠BDC=60°.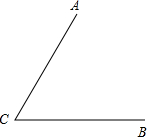 如图两条公路CA与CB,B,C是两个村庄,现在要建一个菜场,使它到两个村庄的距离相等而且还要使它到两条公路的距离也相等,用尺规作图画出菜场的位置(不写作法)保留作图痕迹.
如图两条公路CA与CB,B,C是两个村庄,现在要建一个菜场,使它到两个村庄的距离相等而且还要使它到两条公路的距离也相等,用尺规作图画出菜场的位置(不写作法)保留作图痕迹.