题目内容
13. 如图,两个同心圆的半径分别为3cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的半径分别为3cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )| A. | 3cm | B. | 4cm | C. | 6cm | D. | 8cm |
分析 连接OC和OB,根据切线的性质:圆的切线垂直于过切点的半径,知OC⊥AB,应用勾股定理可将BC的长求出,从而求出AB的长.
解答  解:连接OC和OB,
解:连接OC和OB,
∵弦AB与小圆相切,
∴OC⊥AB,
在Rt△OBC中,
BC=$\sqrt{O{B}^{2}-O{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4cm,
∴AB=2BC=8cm.
故选D.
点评 此题考查了切线的性质,勾股定理,以及垂径定理,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.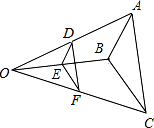 如图,D,E,F分别是OA,OB,OC的中点,下面的说法中:
如图,D,E,F分别是OA,OB,OC的中点,下面的说法中:
①△ABC与△DEF是位似图形;
②△ABC与△DEF的相似比为1:2;
③△ABC与△DEF的周长之比为2:1;
④△ABC与△DEF的面积之比为4:1.
正确的是( )
 如图,D,E,F分别是OA,OB,OC的中点,下面的说法中:
如图,D,E,F分别是OA,OB,OC的中点,下面的说法中:①△ABC与△DEF是位似图形;
②△ABC与△DEF的相似比为1:2;
③△ABC与△DEF的周长之比为2:1;
④△ABC与△DEF的面积之比为4:1.
正确的是( )
| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
 如图,BD是△ABC的角平分线,△ABC的面积为60,AB=15,BC=9,求△ABD的面积.
如图,BD是△ABC的角平分线,△ABC的面积为60,AB=15,BC=9,求△ABD的面积.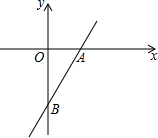 一次函数的图象经过点A(2,0)、B(0,-2$\sqrt{3}$),P为直线AB上的动点,
一次函数的图象经过点A(2,0)、B(0,-2$\sqrt{3}$),P为直线AB上的动点,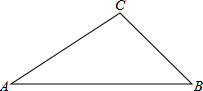 如图,在△ABC中,已知:∠A=30°,∠C=105°,AC=4,求AB和BC的长.
如图,在△ABC中,已知:∠A=30°,∠C=105°,AC=4,求AB和BC的长.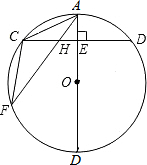 如图,AB为⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,连接AC、AF、CF,求证:△ACH∽△AFC.
如图,AB为⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,连接AC、AF、CF,求证:△ACH∽△AFC.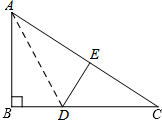 如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,AD是∠BAC的平分线,点E是斜边AC上的一点,且AE=AB,沿△DEC的一个内角平分线折叠,使点C落在DE所在直线上,则折痕的长度为$\frac{12\sqrt{2}}{7}$和$\frac{3\sqrt{5}}{2}$.
如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,AD是∠BAC的平分线,点E是斜边AC上的一点,且AE=AB,沿△DEC的一个内角平分线折叠,使点C落在DE所在直线上,则折痕的长度为$\frac{12\sqrt{2}}{7}$和$\frac{3\sqrt{5}}{2}$.