题目内容
6.阅读材料:为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后设x2-1=y,则(x2-1)2=y2,原方程化为y2-5y+4=0.
解得y1=1,y2=4
当y=1时,x2-1=1.∴x2=2.∴x=±$\sqrt{2}$;
当y=4时,x2-1=4,∴x2=5,∴x=±$\sqrt{5}$.
∴原方程的解为x1=$\sqrt{2}$,x2=-$\sqrt{2}$,x3=$\sqrt{5}$,x4=-$\sqrt{5}$.
解方程:(x2+1)2-(x2+1)-6=0.
分析 将x2+1视为一个整体,然后设x2+1=y,则原方程化为y2-y-6=0.求得方程的解,进一步分析探讨得出答案即可.
解答 解:(x2+1)2-(x2+1)-6=0,
设x2+1=y,
则原方程化为y2-y-6=0.
解得y1=3,y2=-2,
当y=3时,x2+1=3.
解得:x=±$\sqrt{2}$;
当y=-2时,x2+1=-2,
此方程无解.
因此原方程的解为x1=$\sqrt{2}$,x2=-$\sqrt{2}$.
点评 此题考查换元法解一元二次方程,掌握整体的代换方法是解决问题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
16. 如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )
如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )
 如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )
如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )| A. | 70° | B. | 50° | C. | 60° | D. | 30° |
11.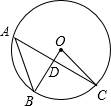 如图,已知A,B,C三点在⊙O上,AC⊥BO于O,∠B=55°,则∠BOC的度数为( )
如图,已知A,B,C三点在⊙O上,AC⊥BO于O,∠B=55°,则∠BOC的度数为( )
 如图,已知A,B,C三点在⊙O上,AC⊥BO于O,∠B=55°,则∠BOC的度数为( )
如图,已知A,B,C三点在⊙O上,AC⊥BO于O,∠B=55°,则∠BOC的度数为( )| A. | 45° | B. | 35° | C. | 70° | D. | 80° |
15.一个三角形的两边长分别为4和7,则此三角形的第三边的取值范围是( )
| A. | 3<x<11 | B. | 4<x<7 | C. | -3<x<11 | D. | x>3 |
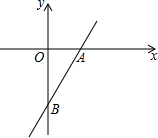 一次函数的图象经过点A(2,0)、B(0,-2$\sqrt{3}$),P为直线AB上的动点,
一次函数的图象经过点A(2,0)、B(0,-2$\sqrt{3}$),P为直线AB上的动点,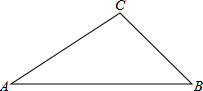 如图,在△ABC中,已知:∠A=30°,∠C=105°,AC=4,求AB和BC的长.
如图,在△ABC中,已知:∠A=30°,∠C=105°,AC=4,求AB和BC的长.