题目内容
8.若a+b+c=0,则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+$\frac{|abc|}{abc}$可能的值的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据a+b+c=0,所以a,b,c三个数中可能有2个负1个正或1个负2个正,分别化简,即可解答.
解答 解:∵a+b+c=0,
∴a,b,c三个数中可能有2个负1个正或1个负2个正,
(1)a,b,c中有两个大于零,一个小于零时,原式=1+1-1-1=0;
(2)当a,b,c中有两个小于零,一个大于零时,原式=-1-1+1+1=0.
故选:A.
点评 本题考查了绝对值,解决本题的关键是确定a,b,c的正负.

练习册系列答案
相关题目
19.已知△ABC中,AB=4,BC=6,那么边AC的长可能是下列哪个值( )
| A. | 11 | B. | 5 | C. | 2 | D. | 1 |
16. 如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )
如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )
 如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )
如图,△ABC≌△DEC,∠A=70°,∠ACB=60°,则∠E的度数为( )| A. | 70° | B. | 50° | C. | 60° | D. | 30° |
 如图,BD是△ABC的角平分线,△ABC的面积为60,AB=15,BC=9,求△ABD的面积.
如图,BD是△ABC的角平分线,△ABC的面积为60,AB=15,BC=9,求△ABD的面积.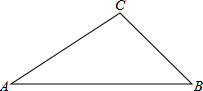 如图,在△ABC中,已知:∠A=30°,∠C=105°,AC=4,求AB和BC的长.
如图,在△ABC中,已知:∠A=30°,∠C=105°,AC=4,求AB和BC的长.