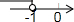
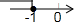题目内容
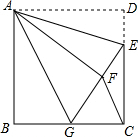 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④∠GAE=45°;⑤S△FGC=3.6.
则正确结论的个数有( )
| A、2 | B、3 | C、4 | D、5 |
考点:翻折变换(折叠问题),正方形的性质
专题:计算题
分析:根据正方形的性质易得AD=CD=BC=6,则由CD=3DE得到CD=2,DE=4,根据折叠的性质得到AF=AD=6,ED=EF=2,∠AFE=∠D=90°,则可根据“HL”证明Rt△ABG≌Rt△AFG;根据全等的性质得BG=FG,设BG=x,则GF=x,CG=6-x,在Rt△CGE中,利用勾股定理得到x2+42=(x+2)2,解得x=3,则BG=CG=3;由GF=CG,根据等腰三角形的性质得∠GFC=∠GCF,利用三角形外角性质得∠BGF=2∠GCF,又由Rt△ABG≌Rt△AFG得到∠BGA=∠FGA,易得∠BGA=∠GCF,于是根据平行线的判定得到AG∥CF;由△ADE沿AE对折至△AFE得∠DAE=∠FAE,由Rt△ABG≌Rt△AFG得∠BAG=∠FAG,所以∠EAF+∠GAF=
(∠DAF+∠BAF)=45°,即∠GAE=45°;作FH⊥GC于H,如图,易证得△GFH∽△GEC,利用相似比计算出FH=
,然后根据三角形面积公式可计算出S△GCF=3.6.
| 1 |
| 2 |
| 12 |
| 5 |
解答:解:∵正方形ABCD中,AB=6,
∴AD=CD=BC=6,
∵CD=3DE,
∴CD=2,DE=4,
∵△ADE沿AE对折至△AFE,
∴AF=AD=6,ED=EF=2,∠AFE=∠D=90°,
∴∠AFG=90°,
在Rt△ABG和Rt△AFG中
,
∴Rt△ABG≌Rt△AFG(HL),所以①正确;
∴BG=FG,
设BG=x,则GF=x,CG=6-x,
在Rt△CGE中,GE=GF+EF=x+2,CE=4,CG=x,
∵CG2+CE2=GE2,
∴x2+42=(x+2)2,解得x=3,
∴BG=3,
∴CG=BC-BG=3,
∴BG=CG,所以②正确;
∵GF=CG=3,
∴∠GFC=∠GCF,
而∠BGF=∠GFC+∠GCF,
∴∠BGF=2∠GCF,
∵Rt△ABG≌Rt△AFG,
∴∠BGA=∠FGA,
∴∠BGF=2∠BGA,
∴∠BGA=∠GCF,
∴AG∥CF,所以③正确;
∵△ADE沿AE对折至△AFE,
∴∠DAE=∠FAE,
∵Rt△ABG≌Rt△AFG,
∴∠BAG=∠FAG,
∴∠EAF+∠GAF=
(∠DAF+∠BAF)=
×90°=45°,
即∠GAE=45°,所以④正确;
作FH⊥GC于H,如图,
∴FH∥EC,
∴△GFH∽△GEC,
∴
=
,即
=
,解得FH=
,
∴S△GCF=
×3×
=3.6,所以⑤正确.
故选D.
∴AD=CD=BC=6,
∵CD=3DE,
∴CD=2,DE=4,
∵△ADE沿AE对折至△AFE,
∴AF=AD=6,ED=EF=2,∠AFE=∠D=90°,
∴∠AFG=90°,
在Rt△ABG和Rt△AFG中
|
∴Rt△ABG≌Rt△AFG(HL),所以①正确;
∴BG=FG,
设BG=x,则GF=x,CG=6-x,
在Rt△CGE中,GE=GF+EF=x+2,CE=4,CG=x,
∵CG2+CE2=GE2,
∴x2+42=(x+2)2,解得x=3,
∴BG=3,
∴CG=BC-BG=3,
∴BG=CG,所以②正确;
∵GF=CG=3,
∴∠GFC=∠GCF,
而∠BGF=∠GFC+∠GCF,
∴∠BGF=2∠GCF,
∵Rt△ABG≌Rt△AFG,
∴∠BGA=∠FGA,
∴∠BGF=2∠BGA,
∴∠BGA=∠GCF,
∴AG∥CF,所以③正确;
∵△ADE沿AE对折至△AFE,

∴∠DAE=∠FAE,
∵Rt△ABG≌Rt△AFG,
∴∠BAG=∠FAG,
∴∠EAF+∠GAF=
| 1 |
| 2 |
| 1 |
| 2 |
即∠GAE=45°,所以④正确;
作FH⊥GC于H,如图,
∴FH∥EC,
∴△GFH∽△GEC,
∴
| FH |
| EC |
| GF |
| GE |
| FH |
| 4 |
| 3 |
| 5 |
| 12 |
| 5 |
∴S△GCF=
| 1 |
| 2 |
| 12 |
| 5 |
故选D.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了正方形的性质、三角形全等和相似的判定与性质、平行线的判定和勾股定理.

练习册系列答案
相关题目
顺次连结正方形各边中点所成的四边形的面积与原正方形的面积之比为( )
A、1:
| ||
B、1:
| ||
| C、1:3 | ||
| D、1:2 |
 如图,矩形ABCD的面积为20cm2,对角线交于点O;以AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )
如图,矩形ABCD的面积为20cm2,对角线交于点O;以AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
下列各式是最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列各点在函数y=2x的图象上的是( )
| A、(2,-1) |
| B、(-1,2) |
| C、(1,2) |
| D、(2,1) |
 反比例函数y=
反比例函数y=| k |
| x |
| A、4 | ||
| B、2 | ||
C、
| ||
| D、1 |
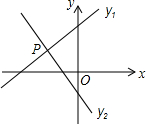 如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是( )
如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是( )