题目内容
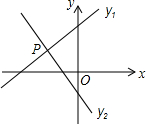 如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是( )
如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集在数轴上表示正确的是( )A、 |
B、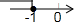 |
C、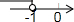 |
D、 |
考点:一次函数与一元一次不等式,在数轴上表示不等式的解集
专题:数形结合
分析:观察函数图象得到当x>-1时,直线y1=x+m都在直线y2=kx-1的上方,即不等式x+m>kx-1的解集为x>-1,然后用数轴表示解集.
解答:解:当x>-1时,y1>y2,
所以关于x的不等式x+m>kx-1的解集为x>-1,
用数轴表示为: .
.
故选D.
所以关于x的不等式x+m>kx-1的解集为x>-1,
用数轴表示为:
 .
.故选D.
点评:本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
如果点P(3,y)在第四象限,则y的取值范围是( )
| A、y>0 | B、y<0 |
| C、y≥0 | D、y≤0 |
若点A(3,a)与点B(b,2)关于x轴对称,则
×(10a)b的结果可表示为( )
| 1 |
| a |
| A、5×105 |
| B、-5×10-7 |
| C、-5×10-5 |
| D、-5×10-9 |
下列各式正确的是( )
A、
| ||||||||
B、
| ||||||||
C、3
| ||||||||
D、
|
分式方程
-
=
的解是( )
| 2014 |
| x-1 |
| 2013 |
| x+1 |
| 4028 |
| x2-1 |
| A、x=1 | B、x=-1 |
| C、无解 | D、有无数个 |
下面的移项正确的是( )
| A、从7+x=13得到x=13+7 |
| B、从5x=4x+8得到5x-4x=8 |
| C、从3x-2=x+1得到3x+x=2+1 |
| D、从8x=7x-2得到8x-7x=2 |
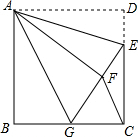 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论: