题目内容
2.当-2≤x≤2时,函数y=kx-k+1(k为常数且k<0)有最大值3,则k的值为-$\frac{2}{3}$.分析 先根据k<0判断出函数的增减性,再由x的取值范围得出x=-2时,y=3,代入函数解析式得出k的值即可.
解答 解:∵k<0,
∴函数y=kx-k+1是减函数.
∵当-2≤x≤2时,函数y=kx-k+1(k为常数且k<0)有最大值3,
∴当x=-2时,y=3,
∴-2k-k+1=3,解得k=-$\frac{2}{3}$.
故答案为:-$\frac{2}{3}$.
点评 本题考查的是一次函数的性质,熟知一次函数的增减性是解答此题的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
10.一次函数y=2x+4交y轴于点A,则点A的坐标为( )
| A. | (0,4) | B. | (4,0) | C. | (-2,0) | D. | (0,-2) |
 如图,将一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′地位置,ED′的延长线与BC相交于点G,若∠EFG=68°,则∠1的度数是136°.
如图,将一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′地位置,ED′的延长线与BC相交于点G,若∠EFG=68°,则∠1的度数是136°. 如图,∠AOC与∠BOC的度数比为5:2,OD平分∠AOB,若∠COD=15°,求∠AOB的度数.
如图,∠AOC与∠BOC的度数比为5:2,OD平分∠AOB,若∠COD=15°,求∠AOB的度数. 如图,直线AB、CD相交于点O,OE⊥AB,点O为垂足,若∠EOD=58°,则∠AOC的度数为32度.
如图,直线AB、CD相交于点O,OE⊥AB,点O为垂足,若∠EOD=58°,则∠AOC的度数为32度.



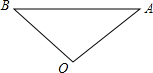 如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )
如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )


