题目内容
 如图,已知平行四边形ABCD中,对角线AC和BD相交于点O.在BC上取点E,使EC=
如图,已知平行四边形ABCD中,对角线AC和BD相交于点O.在BC上取点E,使EC=| 1 |
| 4 |
| BA |
| a |
| BC |
| b |
| a |
| b |
| FD |
| FC |
考点:*平面向量
专题:
分析:由平行四边形ABCD中,
=
,
=
,可求得
,
;易证得△ADF∽△CEF,然后由相似三角形的对应边成比例,求得答案.
| BA |
| a |
| BC |
| b |
| CD |
| AC |
解答:解:∵四边形ABCD是平行四边形,
∴
=
=
,
∴
=
-
=
-
,
=
=
,
∴
=
+
=
+
,
∴AD∥BC,AB∥CD,AD=BC,AB=DC,
∴△ADF∽△CEF,
∴
=
=
,
∵EC=
BC,
∴
=
=
,
∴
=
=
(
+
)=
+
;
=
=
-
.
∴
| CD |
| BA |
| a |
∴
| AC |
| BC |
| BA |
| b |
| a |
| EC |
| 1 |
| 4 |
| BC |
| 1 |
| 4 |
| b |
∴
| ED |
| EC |
| CD |
| 1 |
| 4 |
| b |
| a |
∴AD∥BC,AB∥CD,AD=BC,AB=DC,
∴△ADF∽△CEF,
∴
| DF |
| FE |
| AF |
| FC |
| AD |
| EC |
∵EC=
| 1 |
| 4 |
∴
| DF |
| FE |
| AF |
| FC |
| 1 |
| 4 |
∴
| FD |
| 4 |
| 5 |
| ED |
| 4 |
| 5 |
| 1 |
| 4 |
| b |
| a |
| 1 |
| 5 |
| b |
| 4 |
| 5 |
| a |
| FC |
| 1 |
| 5 |
| AC |
| 1 |
| 5 |
| b |
| 1 |
| 5 |
| a |
点评:此题考查了平面向量的知识以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用,注意掌握平行四边形法则与三角形法则的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
方程
=
去分母后可得( )
| x-3 |
| 2 |
| 1+2x |
| 6 |
| A、3x-3=1+2x |
| B、3x-9=1+2x |
| C、3x-3=2+2x |
| D、3x-12=2+4x |
 如图,在△ABC中,AE是BC边上的高,AD是角平分线,∠B=42°,∠C=68°,分别求∠BAC、∠DAE的度数.
如图,在△ABC中,AE是BC边上的高,AD是角平分线,∠B=42°,∠C=68°,分别求∠BAC、∠DAE的度数. 画图(不用写作法,要保留作图痕迹)尺规作图:求作∠AOB的角平分线OC.
画图(不用写作法,要保留作图痕迹)尺规作图:求作∠AOB的角平分线OC. 如图,把一张长方形纸片ABCD沿EF折叠,C点落在C′处,D点落在D′处,ED′交BC于点G.已知∠EFG=50°,试求∠DEG与∠BGD′的度数.
如图,把一张长方形纸片ABCD沿EF折叠,C点落在C′处,D点落在D′处,ED′交BC于点G.已知∠EFG=50°,试求∠DEG与∠BGD′的度数.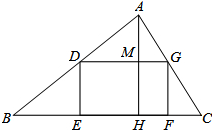 如图,有一块三角形土地,它的底边BC=100m,高AH=80m,某单位要沿底边BC建一座是矩形的大楼,且使矩形的两个端点D、G分别在AB、AC上,当这座大楼的地基面积为1875m2时,求这个矩形沿BC边所占的EF的长.
如图,有一块三角形土地,它的底边BC=100m,高AH=80m,某单位要沿底边BC建一座是矩形的大楼,且使矩形的两个端点D、G分别在AB、AC上,当这座大楼的地基面积为1875m2时,求这个矩形沿BC边所占的EF的长. 已知,如图,等边三角形ABC中,点D,E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE,AD,EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.
已知,如图,等边三角形ABC中,点D,E在边AB上,且∠DCE=30°,请你找出一个条件,使线段DE,AD,EB能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.