题目内容
5．
如图，?ABCD的对角线相交于O，且AB=6，△OCD的周长为23，?ABCD的两条对角线的和是34．
分析 首先由平行四边形的性质可求出CD的长，由条件△OCD的周长为23，即可求出OD+OC的长，再根据平行四边的对角线互相平分即可求出平行四边形的两条对角线的和．
解答 解：∵四边形ABCD是平行四边形，
∴AB=CD=6，
∵△OCD的周长为23，
∴OD+OC=23-6=17，
∵BD=2DO，AC=2OC，
∴平行四边形ABCD的两条对角线的和=BD+AC=2（DO+OC）=34，
故答案为：34．
点评 本题主要考查了平行四边形的基本性质，并利用性质解题．平行四边形的基本性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线互相平分．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
16．下列多项式相乘，不能用平方差公式计算的是（ ）
| A． | （x-2y）（2y-x） | B． | （x-2y）（-x-2y） | C． | （2y-x）（x+2y） | D． | （2y-x）（-x-2y） |
20．下列从左到右的变形中，是因式分解的是（ ）
| A． | x2-6x+9=x（x-6-9） | B． | （a+2）（a-2）=a2-4 | C． | 2a（b-c）=2ab-2bc | D． | y2-4y+4=（y-2）2 |
10．
如图，矩形与⊙O相交，若AB=4，BC=5，DE=3，则EF的长为（ ）
如图，矩形与⊙O相交，若AB=4，BC=5，DE=3，则EF的长为（ ）| A． | 3.5 | B． | 6.5 | C． | 7 | D． | 8 |
17．
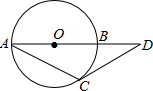如图，已知⊙O的半径为R，AB是⊙O的直径，D是AB延长线上一点，DC是⊙O的切线，C是切点，连结AC．若∠CAB=30°，则BD的长为（ ）
如图，已知⊙O的半径为R，AB是⊙O的直径，D是AB延长线上一点，DC是⊙O的切线，C是切点，连结AC．若∠CAB=30°，则BD的长为（ ）| A． | R | B． | $\sqrt{3}$R | C． | 2R | D． | $\frac{\sqrt{3}}{2}$R |
如图所示，二次函数y=x2-x-6的图象交x轴于A、B两点，交y轴于C点，则△ABC的面积S△ABC=15．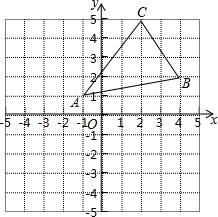
如图，将三角形ABC向左平移3个单位长度，在向下平移4个单位长度，得到三角形A1B1C1．