题目内容
18.计算下列各题(1)$\frac{\sqrt{2}×\sqrt{6}}{\sqrt{8}}$-$\sqrt{\frac{4}{3}}$+$\sqrt{27}$×$\sqrt{8}$
(2)($\sqrt{6}$-2$\sqrt{15}$)×$\sqrt{3}$+${(2\sqrt{2}-1)}^{2}$.
分析 (1)先把各二次根式化简为最简二次根式,再根据二次根式的乘除法则运算,然后合并即可;
(2)先利用二次根式的乘法法则运算,然后合并即可.
解答 解:(1)原式=$\frac{\sqrt{2}×\sqrt{6}}{2\sqrt{2}}$-$\frac{2\sqrt{3}}{3}$+3$\sqrt{3}$×2$\sqrt{2}$
=$\frac{\sqrt{6}}{2}$-$\frac{2\sqrt{3}}{3}$+6$\sqrt{6}$
=$\frac{13\sqrt{6}}{2}$-$\frac{2\sqrt{3}}{3}$;
(2)原式=$\sqrt{6×3}$-2$\sqrt{15×3}$+8-4$\sqrt{2}$+1
=3$\sqrt{2}$-6$\sqrt{5}$+9-4$\sqrt{2}$
=9-$\sqrt{2}$-6$\sqrt{5}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
8.将y=x2向右平移1个单位,再向下平移2单位后,所得表达式是( )
| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=(x-1)2-2 | D. | y=(x+1)2-2 |
13.对于有理数x,y定义一种运算“△”:x△y=ax+by+c,其中a,b,c.为常数,等式右边是通常的加法与乘法运算,已知3△5=15,4△7=28,则1△1的值为( )
| A. | -1 | B. | -11 | C. | 1 | D. | 11 |
3. 如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60 cm,水深为AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,则小动物爬行的最短路线长为( )
如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60 cm,水深为AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,则小动物爬行的最短路线长为( )
 如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60 cm,水深为AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,则小动物爬行的最短路线长为( )
如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60 cm,水深为AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,则小动物爬行的最短路线长为( )| A. | 40 cm | B. | 60 cm | C. | 80 cm | D. | 100 cm |
10.单项式-2πx2y3的系数是( )
| A. | -2 | B. | -2π | C. | 5 | D. | 6 |
7.某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产记为正,减产积为负):
(1)根据记录的数据可知该厂本周实际生产自行车多少辆?
(2)该厂实际每日计划计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元,那么该厂工人这一周的工资总额是多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减产值 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(2)该厂实际每日计划计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元,那么该厂工人这一周的工资总额是多少元?
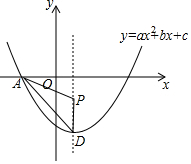 如图,抛物线y=ax2+bx+c的图象与x轴负半轴交于点A(-2,0),顶点D的坐标为(1,-4)
如图,抛物线y=ax2+bx+c的图象与x轴负半轴交于点A(-2,0),顶点D的坐标为(1,-4)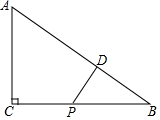 在△ABC中,∠ACB=90°,P为BC中点,PD⊥AB于D,求证:AD2-BD2=AC2.
在△ABC中,∠ACB=90°,P为BC中点,PD⊥AB于D,求证:AD2-BD2=AC2.