题目内容

8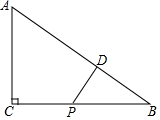．在△ABC中，∠ACB=90°，P为BC中点，PD⊥AB于D，求证：AD2-BD2=AC2．

分析 连接AP得到三个直角三角形，运用勾股定理分别表示出AD2、BD2、AC2进行代换就可以最后得到所要证明的结果．

解答 证明：连接AP，如图所示
AD2-BD2=AP2-PD2-（BP2-PD2）
=AC2+CP2-PD2-BP2+PD2
=AC2+CP2-BP2，
∵P为BC中点，
∴CP=BP，
∴CP2-BP2=0，
∴AD2-BD2=AC2．

点评 此题考查了勾股定理，本题关系比较复杂，三次运用勾股定理进行代换计算就可以出现想要的结果，另外准确作出辅助线也是正确解出的重要因素．

练习册系列答案
相关题目
18．计算下列各题
（1）$\frac{\sqrt{2}×\sqrt{6}}{\sqrt{8}}$-$\sqrt{\frac{4}{3}}$+$\sqrt{27}$×$\sqrt{8}$
（2）（$\sqrt{6}$-2$\sqrt{15}$）×$\sqrt{3}$+${（2\sqrt{2}-1）}^{2}$．
19．计算：
（1）$\root{3}{8}$+$\sqrt{9}$-$\sqrt{1\frac{9}{16}}$+（-1）2015
（2）2$\sqrt{5}$-2（$\sqrt{5}$-$\sqrt{3}$）
16．把抛物线y=（x+3）2向下平移3个单位，再向右平移1个单位，所得到的抛物线解析式是y=（x+2）2-3．
3．在3.14，π，3.212212221，2+$\sqrt{3}$，-$\frac{22}{7}$，2$\sqrt{5}$-6，-5.2121121112…（在相邻两个2之间1的个数逐次加1）中，无理数的个数为（　　）
A．5B．2C．3D．4
13．已知点M（1，-3），点M关于x轴的对称点的坐标是（　　）
A．（-1，3）B．（-1，-3）C．（3，1）D．（1，3）
20．在如图数轴上作出表示-$\sqrt{10}$的点．
17．化简2$\sqrt{2}$-$\frac{3}{\sqrt{2}}$+$\frac{16}{\sqrt{8}}$的结果是（　　）
A．$\frac{9}{2}$$\sqrt{2}$B．-$\frac{7}{2}$$\sqrt{2}$C．$\frac{9}{\sqrt{2}}$D．-$\frac{7}{\sqrt{2}}$
18．在平面直角坐标系中，点P（3，4）到原点的距离是（　　）
A．3B．4C．5D．±5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网