题目内容
13. 如图,△ABC是等边三角形,点E、F分别在边AB和AC上,且AE=BF.
如图,△ABC是等边三角形,点E、F分别在边AB和AC上,且AE=BF.(1)求证:△ABE≌△BCF;
(2)若∠ABE=20°,求∠ACF的度数;
(3)猜测∠BOC的度数并证明你的猜想.
分析 (1)由等边三角形的性质得出AB=CB,∠A=∠ABC=60°,由SAS即可证明△ABE≌△BCF;
(2)由△ABE≌△BCF得到∠ABE=∠BCF,根据角的和差即可得到结论;
(3)由△ABE≌△BCF得到∠ABE=∠BCF,利用外角∠BOC=60°+∠ABE+∠ACF,即可得到结论.
解答 解:(1)∵△ABC是等边三角形,
∴AB=BC,∠A=∠ABC=60°,
在△ABE和△CBF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠ABC}\\{AE=BF}\end{array}\right.$,
∴△ABE≌△BCF(SAS);
(2)∵△ABE≌△BCF,
∴∠BCF=∠ABE=20°,
∵∠ACB=60°,
∴∠ACF=∠ACB-∠BCF=40°;
(3)∵△ABE≌△BCF,
∴∠ABE=∠BCF,
∵∠BFC=∠A+∠ACF=60°+∠ACF,
∴∠BOC=∠BFO+∠ABE=60°+∠ACF+∠ABE=120°.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
3.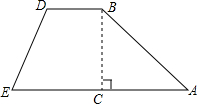 如图是拦水坝的横断面,斜坡AB的水平宽度为12m,斜面坡度为1:2,则斜坡AB的长为( )
如图是拦水坝的横断面,斜坡AB的水平宽度为12m,斜面坡度为1:2,则斜坡AB的长为( )
 如图是拦水坝的横断面,斜坡AB的水平宽度为12m,斜面坡度为1:2,则斜坡AB的长为( )
如图是拦水坝的横断面,斜坡AB的水平宽度为12m,斜面坡度为1:2,则斜坡AB的长为( )| A. | 4$\sqrt{3}$m | B. | 6$\sqrt{5}$m | C. | 12$\sqrt{5}$m | D. | 24m |
1.下列说法正确的是( )
| A. | 掷一枚质地均匀的骰子,“向上一面的点数是6”是必然事件 | |
| B. | 了解一批电视机的使用寿命,适合用普查的方式 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | 在统计中,样本的方差可以近似地反映总体的波动大小 |
2.为执行“两免一补”政策,某地区2015年投入教育经费2700万元,预计2016年、2017年两年共投入6775万元,设这两年投入教育经费的年平均增长百分率为x,那么下面列出的方程正确的是( )
| A. | 2700x2=6775 | B. | 2700(1+x%)2=6775 | ||
| C. | 2700(1+x)2=6775 | D. | 2700(1+x)+2700(1+x)2=6775 |
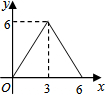
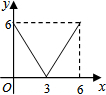

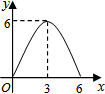
 抛物线y=ax2-2ax-3a与x轴交于A、B两点(其中A在左侧,B在右侧,且经过点C(2,3).
抛物线y=ax2-2ax-3a与x轴交于A、B两点(其中A在左侧,B在右侧,且经过点C(2,3).