题目内容
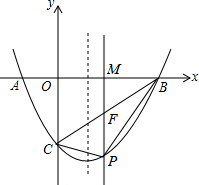 在平面直角坐标系中,A(-1,0),C(0,-2),点B在x轴上,抛物线过A、B、C三点且对称轴为直线x=
在平面直角坐标系中,A(-1,0),C(0,-2),点B在x轴上,抛物线过A、B、C三点且对称轴为直线x=| 1 |
| 2 |
(1)求抛物线解析式;
(2)若P的横坐标为m,用含m的代数式表示线段PF的长;
(3)求△PBC的面积的最大值及此时P的坐标.
考点:二次函数综合题
专题:
分析:(1)先根据抛物线的对称性确定B点坐标为(2,0),则可设交点式y=a(x+1)(x-2),然后把C(0,-2)代入可计算出a的值为1,从而得到抛物线解析式为y=x2-x-2;
(2)先利用待定系数法求出直线BC的解析式为y=x-2,再根据一次函数图象上点的坐标特征和二次函数图象上点的坐标特征得到F点的坐标为(m,m-2),P点坐标为(m,m2-m-2),于是用F点与P点的纵坐标之差得到线段PF;
(3)过点P作l∥BC,交y轴于Q点,如图,只有当l与抛物线只有唯一的公共点P时,△PBC的面积最大;设此时l的解析式为y=x+n,所以方程组
有唯一一组解,消去y得到关于x的方程x2-2x-2-n=0,利用△=0解得n=-3,同时解得x1=x2=1,利用直线l的解析式y=x-3可确定此时P点坐标为(1,-2),再计算出S△BCQ=1,由于l∥BC,所以S△PBC=S△BCQ=1.
(2)先利用待定系数法求出直线BC的解析式为y=x-2,再根据一次函数图象上点的坐标特征和二次函数图象上点的坐标特征得到F点的坐标为(m,m-2),P点坐标为(m,m2-m-2),于是用F点与P点的纵坐标之差得到线段PF;
(3)过点P作l∥BC,交y轴于Q点,如图,只有当l与抛物线只有唯一的公共点P时,△PBC的面积最大;设此时l的解析式为y=x+n,所以方程组
|
解答:解:(1)∵抛物线过A(-1,0)和点B,且对称轴为直线x=
,
∴B点坐标为(2,0),
设抛物线解析式为y=a(x+1)(x-2),
把C(0,-2)代入得a•1•(-2)=-2,解得a=1,
∴抛物线解析式为y=(x+1)(x-2)=x2-x-2;
(2)设直线BC的解析式为y=kx+b,
把B(2,0)、C(0,-2)代入得
,解得
,
∴直线BC的解析式为y=x-2,
∵过P作y轴的平行线交BC于F,
∴当P的横坐标为m时,F点的坐标为(m,m-2),P点坐标为(m,m2-m-2),
∴PF=m-2-(m2-m-2)=-m2+2m(0<m<2);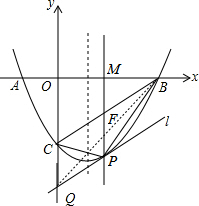
(3)过点P作l∥BC,交y轴于Q点,如图,
∵当l与抛物线只有唯一的公共点P时,△PBC的面积最大,设此时l的解析式为y=x+n,
∴方程组
有唯一一组解,即x2-x-2=x+n有相等的实数解,
整理得x2-2x-2-n=0,△=(-2)2-4(-2-n)=0,解得n=-3,
∴x1=x2=1,
∴直线l的解析式为y=x-3,
∵当x=1时,y=x-3=-2,
∴此时P点坐标为(1,-2),
∵Q点坐标为(0,-3),
∴S△BCQ=
OB•CQ=
×2×1=1,
∵l∥BC,
∴S△PBC=S△BCQ=1,
即△PBC的面积的最大值为1,此时P的坐标为(1,-2).
| 1 |
| 2 |
∴B点坐标为(2,0),
设抛物线解析式为y=a(x+1)(x-2),
把C(0,-2)代入得a•1•(-2)=-2,解得a=1,
∴抛物线解析式为y=(x+1)(x-2)=x2-x-2;
(2)设直线BC的解析式为y=kx+b,
把B(2,0)、C(0,-2)代入得
|
|
∴直线BC的解析式为y=x-2,
∵过P作y轴的平行线交BC于F,
∴当P的横坐标为m时,F点的坐标为(m,m-2),P点坐标为(m,m2-m-2),
∴PF=m-2-(m2-m-2)=-m2+2m(0<m<2);

(3)过点P作l∥BC,交y轴于Q点,如图,
∵当l与抛物线只有唯一的公共点P时,△PBC的面积最大,设此时l的解析式为y=x+n,
∴方程组
|
整理得x2-2x-2-n=0,△=(-2)2-4(-2-n)=0,解得n=-3,
∴x1=x2=1,
∴直线l的解析式为y=x-3,
∵当x=1时,y=x-3=-2,
∴此时P点坐标为(1,-2),
∵Q点坐标为(0,-3),
∴S△BCQ=
| 1 |
| 2 |
| 1 |
| 2 |
∵l∥BC,
∴S△PBC=S△BCQ=1,
即△PBC的面积的最大值为1,此时P的坐标为(1,-2).
点评:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质;会利用待定系数法求函数解析式;会利用方程组的问题确定两函数图象的交点坐标;会根据三角形面积公式计算三角形的面积.

练习册系列答案
相关题目
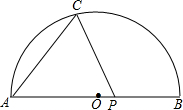 如图,AB为半圆的直径,AB=10,点O到弦AC的距离为4,点P从B出发沿BA方向向点A以每秒1个单位长度的速度运动,连接CP,经过
如图,AB为半圆的直径,AB=10,点O到弦AC的距离为4,点P从B出发沿BA方向向点A以每秒1个单位长度的速度运动,连接CP,经过
 如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).用砌60米长的墙的材料,当矩形的长BC为多少米时,矩形花园的面积为300平方米;能否围成480平方米的矩形花园,为什么?
如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).用砌60米长的墙的材料,当矩形的长BC为多少米时,矩形花园的面积为300平方米;能否围成480平方米的矩形花园,为什么?