题目内容
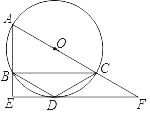
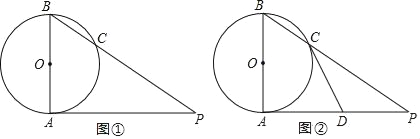
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,连OC,求∠BOC的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
【答案】(1)∠BOC=70°;(2)详见解析.
【解析】
(1)连接OC.已知AP是⊙O的切线,根据切线的性质可得∠PAB=90°,再由直角三角形的两锐角互余求出∠B=55°,最后利用等腰三角形的性质及三角形的内角和定理即可解决问题;(2)如图②中,连接OC,OD,AC.根据已知条件易证△ODC≌△ODA,由全等三角形的性质可得∠OCD=∠OAD=90°,由此即可证得结论.
解:(1)如图①中,连接OC.
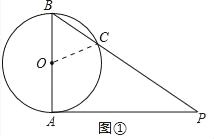
∵PA是⊙O的切线,
∴PA⊥AB,
∴∠PAB=90°,
∵∠P=35°,
∴∠B=55°,
∵OB=OC,
∴∠B=∠OCB=55°,
∴∠BOC=180°﹣55°﹣55°=70°.
(2)如图②中,连接OC,OD,AC.
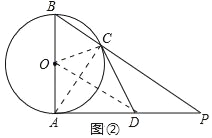
∵AB是直径,
∴∠ACB=∠ACP=90°,
∵AD=DP,
∴DC=DA=DB,
∵OA=OC,OD=OD,
∴△ODC≌△ODA(SSS),
∴∠OCD=∠OAD=90°,
∴OC⊥CD,
∴DC是⊙O的切线.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目