��Ŀ����
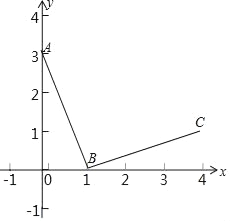
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A��0��3����B��1��0��������BA�����߶�BA�Ƶ�B˳ʱ����ת90���õ��߶�BC������������y��![]() ��ͼ��G������C��
��ͼ��G������C��
��1����ֱ��д����C�����꼰k��ֵ��
��2������P��ͼ��G�ϣ��ҡ�POB����BAO�����P�����ꣻ
��3���ڣ�2���������£���Q��0��m��Ϊy����������һ�㣬����Q��x���ƽ������ͼ��G���ڵ�M����ֱ��OP���ڵ�N������M�ڵ�N��࣬���ͼ��ֱ��д��m��ȡֵ��Χ��
���𰸡�(1)��C�����꣨4��1����k��ֵ��4�� (2) P��2![]() ��
��![]() ����(3)
����(3) ![]()
��������
��1����C����CH��x����H����ͼ��������ת�����ʵ�BA=BC����ABC=90������֤����ABO�ա�BCH�õ�CH=OB=1��BH=OA=3����C��4��1����Ȼ���C���������y=![]() (x��0)�пɼ����k��ֵ��
(x��0)�пɼ����k��ֵ��
��2����������C�ķ���������y=![]() (x��0)�IJ�ͼ�����������P��ͼ��G�ϣ��������������ε��ж������ʼ��ɵõ����ۣ�
(x��0)�IJ�ͼ�����������P��ͼ��G�ϣ��������������ε��ж������ʼ��ɵõ����ۣ�
��3����Q��0��m�����õ�OQ=m���õ�M��![]() ��m����N��3m��m����������M�ڵ�N��࣬�в���ʽ���ɵõ����ۣ�
��m����N��3m��m����������M�ڵ�N��࣬�в���ʽ���ɵõ����ۣ�
�⣺(1) ��C����CH��x����H����ͼ��
���߶�AB�Ƶ�B˳ʱ����ת90�����õ��߶�BC��
��BA=BC����ABC=90����
�ߡ�ABO+��CBH=90������ABO+��BAO=90����
���BAO=��CBH��
����ABO����BCH��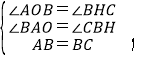
���ABO�ա�BCH��AAS����
��CH=OB=1��BH=OA=3��
��C��4��1����
�ߵ�C���ں���y=![]() ��x��0����ͼ���ϣ�
��x��0����ͼ���ϣ�
��k=4��1=4��
�ʴ�Ϊ����C�����꣨4��1����k��ֵ��4
(2)��O��OP��BC��![]() �ڵ�P����P��PE��x����E��
�ڵ�P����P��PE��x����E��
�ߡ�POE=��OAB����AOB=��PEO��
���OAB�ס�OHP��
��PE��OE=OB��OA=1��3���ߵ�P��![]() ��
��
��![]()
![]()
��P��2![]() ��
��![]() ��
��
(3) ![]() �����ɣ�
�����ɣ�
��Q��0��m����
��OQ=m��
��QM��x�ᣬ��ͼ��G���ڵ�M����ֱ��OP���ڵ�N��
��M��![]() ��m����N��3m��m����
��m����N��3m��m����
�ߵ�M�ڵ�N��࣬
��![]() ��3m��
��3m��
��m��0��
��m��![]() ��
��

����Ŀ�����κ���y��ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ���±����������½��ۣ�
x | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 | 5 | �� |
y | �� | 12 | 5 | 0 | ��3 | ��4 | ��3 | 0 | 5 | 12 | �� |
�ٶ��κ���y��ax2+bx+c����Сֵ����СֵΪ��3���ڵ���![]() ��x��2ʱ��y��0���۶��κ���y��ax2+bx+c��ͼ����x�����������㣬�����Ƿֱ���y������ࣻ�ܵ�x��1ʱ��y��x���������С����������ȷ�����У� ��
��x��2ʱ��y��0���۶��κ���y��ax2+bx+c��ͼ����x�����������㣬�����Ƿֱ���y������ࣻ�ܵ�x��1ʱ��y��x���������С����������ȷ�����У� ��
A. 4�� B. 3�� C. 2�� D. 1��