Question

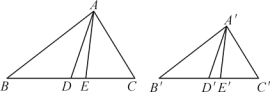
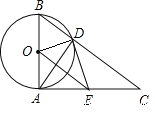
【题目】在△ABC中，∠ACB＝90°，点D、E分别在边BC、AC上，AC＝3AE，∠CDE＝45°（如图），△DCE沿直线DE翻折，翻折后的点C落在△ABC内部的点F，直线AF与边BC相交于点G，如果BG＝AE，那么tanB＝_____．

Answer 1

【答案】

【解析】

设AE＝k＝BG，AC＝3k，（k≠0），可得EC＝2k，由折叠的性质可得EF＝EC＝2k，∠FED＝∠DEC＝45°，根据相似三角形的性质可得，即GC＝3EF＝6k，

则可求tanB的值．

解：如图，

∵∠ACB＝90°，∠CDE＝45°，

∴∠DEC＝45°

∵AC＝3AE

∴设AE＝k＝BG，AC＝3k，（k≠0）

∴EC＝2k，

∵折叠

∴EF＝EC＝2k，∠FED＝∠DEC＝45°

∴∠FEC＝90°，且∠ACB＝90°

∴EF∥BC

∴△AEF∽△ACG

∴

∴GC＝3EF＝6k，

∴BC＝BG＋GC＝7k，

∴tanB＝＝

故答案为：