Question

【题目】顺次连接平面直角坐标系xOy中，任意的三个点P，Q，G．如果∠PQG＝90°，那么称∠PQG为“黄金角”．

已知：点A（0，3），B（2，3），C（3，4），D（4，3）．

（1）在A，B，C，D四个点中能够围成“黄金角”的点是　 　；

（2）当时，直线y＝kx+3（k≠0）与以OP为直径的圆交于点Q（点Q与点O，P不重合），当∠OQP是“黄金角”时，求k的取值范围；

（3）当P（t，0）时，以OP为直径的圆与△BCD的任一边交于点Q，当∠OQP是“黄金角”时，求t的取值范围．

Answer 1

【答案】（1）B，C，D；（2）﹣≤k＜0；（3）6≤t≤.

【解析】

(1)描点,顺次连接，看有几个90°角.

（2）根据直线与圆有交点，分为相切和相交两种情况进行求解.当相切时，根据切线的性质及J（,0），F（0，3）求出∠JFO＝∠JFQ＝30°，从而求∠OFH＝60°，最终求的H点的坐标代入直线方程即可.当相交时都符合条件，最终求出k的范围

（3）根据（2）的分析，找出圆与三角形相切或相交的两种极限情况求出的值，即为t边界情况.

解：（1）观察图象可知：∠BCD＝90°，

∴在A，B，C，D四个点中能够围成“黄金角”的点是B，C，D；

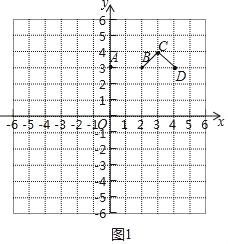
故答案为B，C，D．

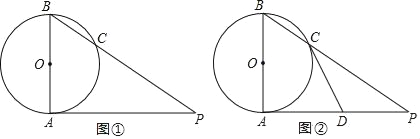
（2）如图2中，当直线y＝kx+3与⊙J相切时，设直线y＝kx+3交y轴于点F，交x轴于点H，切点为Q，连接FJ．

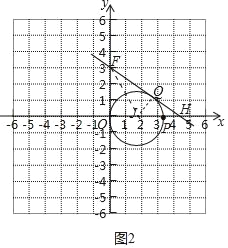
∵FO，FQ是切线，

∴∠JFO＝∠JFQ，

∵J（，0），F（0，3），

∴tan∠JFO＝

∴∠JFO＝∠JFQ＝30°，

∴∠OFH＝60°，

∴OH＝OF＝3，

∴H（3，0），

把H（3，0）代入y＝kx+3，

得到k＝﹣，

观察图象可知：当直线y＝kx+3与⊙j有交点时，∠OQP是“黄金角”（点Q与点O，P不重合），

∴﹣≤k＜0．

（3）如图3中，设以OP为直径的圆的圆心为J．

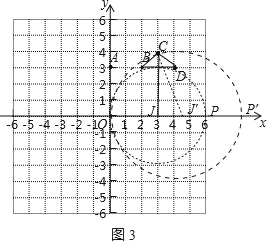
由题意可知当以OP为直径的圆与△BCD的边有交点时，∠OQP是“黄金角”，

当⊙J与△BCD的边相切时，J（3，0）．此时P（6，0），t＝6．

当⊙J′经过等C时，连接CJ′，CJ．设OJ′＝CJ′＝r，

在Rt△CJJ′中，r2＝（r﹣3）2+42，

解得r＝，

∴OP′＝，

∴P′（，0），

观察图象可知：当6≤t≤时，∠OQP是“黄金角”．