题目内容
17.已知(x2+y2)(6-x2-y2)=-7,x2+y2+1=8.分析 设a=x2+y2,把方程转化为a(6-a)=-7,求得方程的解,进一步非负数的性质得出x2+y2的数值,代入求得答案即可.
解答 解:设a=x2+y2,
则原方程为a(6-a)=-7,
a2-6a-7=0,
解得:a=7,或a=-1,
∵x2+y2≥0,
∴x2+y2=7,
则x2+y2+1=8.
故答案为:8.
点评 此题考查换元法解一元二次方程,非负数的性质,掌握整体代换的思想是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
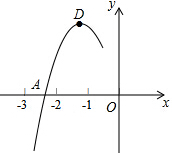 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则方程ax2+bx+c-2=0有两个相等实数根.
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则方程ax2+bx+c-2=0有两个相等实数根.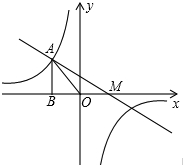 如图,点A(-2,b)是函数y=$\frac{k}{x}$的图象上的点,过点A作AB⊥x轴于点B,△AOB的面积为2,若一次函数y=ax+1的图象经过点A且与x轴交于点M,则AO:AM=$\sqrt{2}$:$\sqrt{5}$.
如图,点A(-2,b)是函数y=$\frac{k}{x}$的图象上的点,过点A作AB⊥x轴于点B,△AOB的面积为2,若一次函数y=ax+1的图象经过点A且与x轴交于点M,则AO:AM=$\sqrt{2}$:$\sqrt{5}$. 如图所示,已知∠1+∠2=90°,AB⊥BC,垂足为点B.试证明:BC∥AD.
如图所示,已知∠1+∠2=90°,AB⊥BC,垂足为点B.试证明:BC∥AD.