题目内容
7.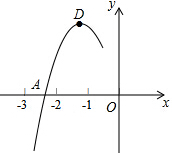 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则方程ax2+bx+c-2=0有两个相等实数根.
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则方程ax2+bx+c-2=0有两个相等实数根.
分析 抛物线y=ax2+bx+c向下平移2个单位得到y=ax2+bx+c-2,顶点D的坐标为(-1,2)从而可知y=ax2+bx+c-2的顶点在x轴上,从而可得到方程的解得情况.
解答 解:令y=ax2+bx+c-2.
∵y=ax2+bx+c向下平移2个单位得到y=ax2+bx+c-2,且抛物线y=ax2+bx+c顶点D的坐标为(-1,2),
∴抛物线y=ax2+bx+c-2的顶点坐为(-1,0).
∴方程ax2+bx+c-2=0有两个相等的实数根.
故答案为:有两个相等.
点评 本题主要考查的是抛物线与x轴的交点坐标,将方程问题转化为函数问题是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 已知:如图所示,求直线AB的解析式.
已知:如图所示,求直线AB的解析式. 某居民小区有一朝向为正南方向的居民楼(如图),该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面24米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为32°时.
某居民小区有一朝向为正南方向的居民楼(如图),该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面24米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为32°时.