题目内容
19.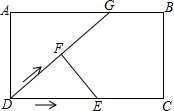 如图所示,在矩形ABCD中,AB=5cm,AD=3cm,G为边AB上一点,GB=1cm,动点E、F同时从点D出发,点F沿射线DG-GB-BC运动到点C时停止,点E沿DC运动到点C时停止,它们运动的速度都是1cm/s,若E、F同时运动t s时,△DEF的面积为5cm2,则t的值为$\frac{5\sqrt{6}}{3}$或7.
如图所示,在矩形ABCD中,AB=5cm,AD=3cm,G为边AB上一点,GB=1cm,动点E、F同时从点D出发,点F沿射线DG-GB-BC运动到点C时停止,点E沿DC运动到点C时停止,它们运动的速度都是1cm/s,若E、F同时运动t s时,△DEF的面积为5cm2,则t的值为$\frac{5\sqrt{6}}{3}$或7.
分析 分三种情况:①点F在DG上;②点F在BG上;③点F在BC上;根据等量关系:△DEF的面积为5cm2,列出方程求解即可.
解答 解:在Rt△ADG中,DG=$\sqrt{{3}^{2}+(5-1)^{2}}$=5,
①点F在DG上,依题意有
$\frac{1}{2}$t×$\frac{3}{5}$t=5,
解得t=±$\frac{5\sqrt{6}}{3}$(负值舍去);
②点F在BG上,依题意有
$\frac{1}{2}$×5×3≠5,
此种情况不存在,
③点F在BC上,依题意有
$\frac{1}{2}$×5×[3-(t-6)]=5,
解得t=7.
答:t的值为$\frac{5\sqrt{6}}{3}$或7.
故答案为:$\frac{5\sqrt{6}}{3}$或7.
点评 考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.注意分类思想的运用.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
4.小敏同学跳绳7次测试成绩如下(单位:分):8.5,7,9,8,9,8.5,9.这组数据的中位数和众数分别为( )
| A. | 8,9 | B. | 9,8.5 | C. | 8.5,9 | D. | 8,8.5 |
8.某公司的物流业务原来由A运输队承接,已知其收费标准y(元)与运输所跑路程x(公里)之间是某种函数关系.其中部分数据如表所示:
(1)写出y(元)关于x(公里)的函数解析式yA=2.5x;(不需写出定义域)
(2)由于行业竞争激烈,现B运输队表示:若公司每次支付200元的汽车租赁费,则可按每公里0.9元收费.请写出B运输队每次收费y(元)关于所跑路程x(公里)的函数解析式yB=200+0.9x;(不需写出定义域)
(3)如果该公司有一笔路程500公里的运输业务,请通过计算说明应该选择哪家运输队?
| x(公里) | 80 | 120 | 180 | 200 | … |
| y(元) | 200 | 300 | 450 | 500 | … |
(2)由于行业竞争激烈,现B运输队表示:若公司每次支付200元的汽车租赁费,则可按每公里0.9元收费.请写出B运输队每次收费y(元)关于所跑路程x(公里)的函数解析式yB=200+0.9x;(不需写出定义域)
(3)如果该公司有一笔路程500公里的运输业务,请通过计算说明应该选择哪家运输队?
 已知圆O,
已知圆O, 如图,在△ABC中,已知AB=AC,CE⊥BD,CD=CB,求证:
如图,在△ABC中,已知AB=AC,CE⊥BD,CD=CB,求证: