题目内容
9.整数k为何值时,二元一次方程组$\left\{\begin{array}{l}{2x-y=3k+1}\\{3x+y=2k-5}\end{array}\right.$的解均为非正数.分析 把k看做已知数表示出x与y,根据方程组的解为非正数确定出整数k的值即可.
解答 解:$\left\{\begin{array}{l}{2x-y=3k+1①}\\{3x+y=2k-5②}\end{array}\right.$,
①+②得:5x=5k-4,即x=$\frac{5k-4}{5}$,
把x=$\frac{5k-4}{5}$代入①得:y=-$\frac{5k+13}{5}$,
由x与y为非正数,得到$\left\{\begin{array}{l}{\frac{5k-4}{5}≤0}\\{-\frac{5k+13}{5}≤0}\end{array}\right.$,
解得:-$\frac{13}{5}$≤k≤$\frac{4}{5}$,
则整数k的值为-2,-1,0.
点评 此题考查了二元一次方程组的解,以及解一元一次不等式,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
17.已知二次函数y=x2-2mx+m2+3(m为常数),下列结论正确的是( )
| A. | 当m=0时,二次函数图象的顶点坐标为(0,0) | |
| B. | 当m<0时,二次函数图象的对称轴在y轴右侧 | |
| C. | 设二次函数的图象与y轴交点为A,过A作x轴的平行线,交图象于另一点B,抛物线的顶点为C,则△ABC的面积为m3 | |
| D. | 该函数图象沿y轴向下平移6个单位后,图象与x轴两交点之间的距离为2$\sqrt{3}$ |
4.为了使圆心距为4cm的两圆内切,其中一个圆的半径为3cm,则另一个圆的半径值是( )
| A. | 1cm | B. | 3cm | C. | 5cm | D. | 7cm |
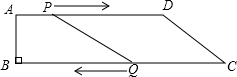 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=9cm,BC=13cm.点P从点A出发,以1cm/s的速度向终点D运动;点Q从点C同时出发,以2cm/s的速度向终点B运动,当其中一个动点到达终点时,另一个点也随之停止运动.设运动时间为ts.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=9cm,BC=13cm.点P从点A出发,以1cm/s的速度向终点D运动;点Q从点C同时出发,以2cm/s的速度向终点B运动,当其中一个动点到达终点时,另一个点也随之停止运动.设运动时间为ts.
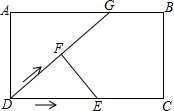 如图所示,在矩形ABCD中,AB=5cm,AD=3cm,G为边AB上一点,GB=1cm,动点E、F同时从点D出发,点F沿射线DG-GB-BC运动到点C时停止,点E沿DC运动到点C时停止,它们运动的速度都是1cm/s,若E、F同时运动t s时,△DEF的面积为5cm2,则t的值为$\frac{5\sqrt{6}}{3}$或7.
如图所示,在矩形ABCD中,AB=5cm,AD=3cm,G为边AB上一点,GB=1cm,动点E、F同时从点D出发,点F沿射线DG-GB-BC运动到点C时停止,点E沿DC运动到点C时停止,它们运动的速度都是1cm/s,若E、F同时运动t s时,△DEF的面积为5cm2,则t的值为$\frac{5\sqrt{6}}{3}$或7.