题目内容
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣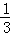 ,y2)在该图象上,则y1>y2.其中正确的结论是 (填入正确结论的序号).
,y2)在该图象上,则y1>y2.其中正确的结论是 (填入正确结论的序号).

②④
【考点】二次函数图象与系数的关系.
【分析】由图象可先判断a、b、c的符号,可判断①;由x=﹣1时函数的图象在x轴下方可判断②;由对称轴方程可判断③;由对称性可知当x=2时,函数值大于0,可判断④;结合二次函数的对称性可判断⑤;可得出答案.
【解答】解:
∵二次函数开口向下,且与y轴的交点在x轴上方,
∴a<0,c>0,
∵对称轴为x=1,
∴﹣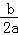 =1,
=1,
∴b=﹣2a>0,
∴abc<0,
故①、③都不正确;
∵当x=﹣1时,y<0,
∴a﹣b+c<0,
故②正确;
由抛物线的对称性可知抛物线与x轴的另一交点在2和3之间,
∴当x=2时,y>0,
∴4a+2b+c>0,
故④正确;
∵抛物线开口向下,对称轴为x=1,
∴当x<1时,y随x的增大而增大,
∵﹣2<﹣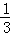 ,
,
∴y1<y2,
故⑤不正确;
综上可知正确的为②④,
故答案为:②④.
【点评】本题主要考查二次函数的性质,掌握二次函数的开口方向、对称轴、增减性是解题的关键,注意数形结合.

练习册系列答案
相关题目
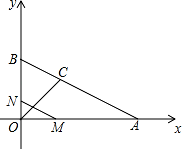
 中,
中, 分别是
分别是 的中点,
的中点, 平分
平分 ,交
,交 于点
于点 ,若
,若 ,则
,则 的长是( ).
的长是( ). A.2 B.3 C.
A.2 B.3 C. D.4
D.4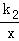 的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )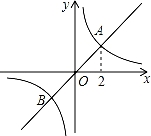
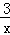 与函数y=
与函数y=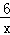 在第一象限内的图象,点P是y=
在第一象限内的图象,点P是y=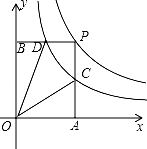

 )
)