��Ŀ����
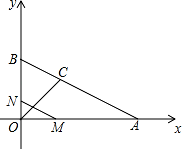
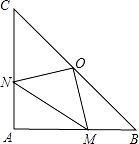
��ͼ����֪�� A��4��0����B��0��2������AOB ��ƽ���߽� AB �� C������ M �� O ���������ÿ �� 2 ����λ���ȵ��ٶ��� x ����� A �������˶���ͬʱ���� N �� O ���������ÿ�� 1 ����λ���ȵ� �ٶ��� y ����� B �������˶����� P��Q Ϊ�� M��N ����ֱ�� OC �ĶԳƵ㣬�� M �˶���ʱ��Ϊ t
��0��t��2���룮
��1���� C ������꣬��ֱ��д���� P��Q �����꣨�ú� t �Ĵ���ʽ��ʾ���� �˶������У�
���Ƿ����ijһʱ��ʹ����CPQ Ϊ����ֱ�������Σ������ڣ���� t ��ֵ���������ڣ���˵�����ɣ�
������CPQ ����OAB �ص����ֵ����Ϊ S������ S ���� t �ĺ�����ϵʽ��
�����㡿һ�κ����ۺ��⣮
����������1���ȸ��� OC ����AOB ��ƽ���ߵó� OC �Ľ���ʽΪ y=x�������ô���ϵ�������ֱ�� AB �Ľ���ʽ���ʿɵó� C �����꣬�� t ��ʾ���� M ��� N �����꣬������ԳƵ����ʿɵó� P�� Q ��������ꣻ
�ٷ� CP=PQ��PQ=QC �� CP=CQ ��������������ۼ��ɣ�
���� 0��t��1 ʱ��S=S��POC+S��OQC��S��OPQ���� 1��t��2 ʱ���� PQ �� AB ���ڵ� D�����ص������� ��Ϊ��CDQ ��������ݴ˿ɵó����ۣ�
����𡿽⣺��1����OC ����AOB ��ƽ���ߣ�
��OC �Ľ���ʽΪ y=x��

 ���� ���� ����ð�������������� �������У� ��
���� ���� ����ð�������������� �������У� ��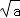 ��a��
��a�� 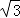 ����0���� b=2��a���� b ��ȡֵ��Χ��
����0���� b=2��a���� b ��ȡֵ��Χ�� 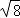

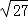 A�� B��
A�� B�� 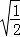 C�� D��
C�� D��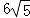
 ��
��
 ��y2���ڸ�ͼ���ϣ���y1��y2��������ȷ�Ľ�������������������������ȷ���۵���ţ���
��y2���ڸ�ͼ���ϣ���y1��y2��������ȷ�Ľ�������������������������ȷ���۵���ţ���