题目内容
13.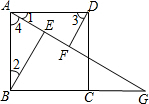 如图,四边形ABCD是边长为4的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.
如图,四边形ABCD是边长为4的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4.(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
分析 (1)由正方形的性质得出AB=AD=4,AD∥BC,由ASA证明△ABE≌△DAF即可;
(2)由平行线的性质得出∠1=∠AGB=30°,得出∠4=60°,得出∠1=∠2=30°,∠3=∠4=60°,证出∠AFD=∠AEB=90°,由含30°角的直角三角形的性质得出DF=2,AE=2,得出AF=2$\sqrt{3}$,即可求出EF的长..
解答 (1)证明:∵四边形ABCD是正方形
∴AB=AD=4,AD∥BC,
在△ABE和△DAF中,
$\left\{\begin{array}{l}{∠2=∠1}&{\;}\\{AB=DA}&{\;}\\{∠4=∠3}&{\;}\end{array}\right.$,
∴△ABE≌△DAF;
(2)解:∵AD∥BG,
∴∠1=∠AGB=30°,
∴∠4=90°-30°=60°,
∴∠1=∠2=30°,∠3=∠4=60°,
∴∠AFD=∠AEB=90°,
∴DF=$\frac{1}{2}$AD=2,AE=$\frac{1}{2}$AB=2,
∴AF=$\sqrt{3}$DF=2$\sqrt{3}$,
∴EF=AF-AE=2$\sqrt{3}$-2.
点评 本题考查了正方形的性质、全等三角形的判定、含30°角的直角三角形的性质、三角函数;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
4.如图,矩形纸片按图(1)中的虚线第一次折叠得图(2),折痕与矩形一边的形成的∠1=65°,再按图(2)中的虚线进行第二折叠得到图(3),则∠2的度数为( )
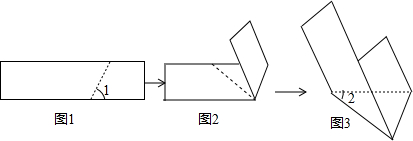

| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
1.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (ab)3=ab3 | C. | (a2)3=a6 | D. | a6÷a2=a3 |
8.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
从上表可知,下列说法中错误的是( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | 抛物线与x轴的一个交点为(3,0) | B. | 在对称轴左侧,y随x增大而增大 | ||
| C. | 抛物线的对称轴是直线x=$\frac{1}{2}$ | D. | 函数y=ax2+bx+c的最大值为6 |
5.下列各组单项式中,不是同类项的是( )
| A. | 0.4x2y与0.3xy2 | B. | 2a2b与5ba2 | C. | 13与-$\frac{3}{2}$ | D. | -3x与7x |
2.如果分式$\frac{{x}^{2}-9}{3x+9}$的值为零,则x的值为( )
| A. | 9 | B. | 3 | C. | -3 | D. | ±3 |
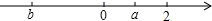 看数轴,化简:|a|-|b|+|a-2|.
看数轴,化简:|a|-|b|+|a-2|. 如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC(阴影部分)的面积为2π;用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r=$\frac{{\sqrt{3}}}{3}$.
如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC(阴影部分)的面积为2π;用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r=$\frac{{\sqrt{3}}}{3}$. 如图,在四边形ABCD中,AD∥BC,EF过AC的中点O,分别交AD,BC于点E,F.
如图,在四边形ABCD中,AD∥BC,EF过AC的中点O,分别交AD,BC于点E,F.