题目内容
15.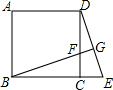 如图,在正方形ABCD中,延长BC到E,在CD上截取CF=CE,延长BF交DE于G.求证:BG⊥DE.
如图,在正方形ABCD中,延长BC到E,在CD上截取CF=CE,延长BF交DE于G.求证:BG⊥DE.
分析 首先证明△BCF≌△DCE可得∠FBC=∠CDE,再由∠FBC+∠BFC=90°,∠DFG=∠BFC,可得BG⊥DE.
解答 证明:∵四边形ABCD是正方形,
∴BC=DC,∠DCB=90°,
在△BCF和△DCE中,
$\left\{\begin{array}{l}{CF=CE}\\{∠BCF=∠FCE}\\{BC=CD}\end{array}\right.$,
∴△BCF≌△DCE(SAS),
∴∠FBC=∠CDE,
∵∠DCB=90°
∴∠FBC+∠BFC=90°,
∵∠DFG=∠BFC,
∴∠GFD+∠FDG=90°,
∴BG⊥DE.
点评 此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形对应角相等.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式$\sqrt{a-2}$+(b-3)2=0,(c-4)2≤0
如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式$\sqrt{a-2}$+(b-3)2=0,(c-4)2≤0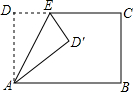 将长方形ABCD沿AE折叠,得到如图所示的图形,若∠CED′=50°,则∠EAB的大小是65°.
将长方形ABCD沿AE折叠,得到如图所示的图形,若∠CED′=50°,则∠EAB的大小是65°. 如图,已知△ABC是等边三角形,BE=CD,EH⊥AD于H,DG∥EH交CE于G,求证:EG=2HD.
如图,已知△ABC是等边三角形,BE=CD,EH⊥AD于H,DG∥EH交CE于G,求证:EG=2HD.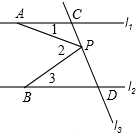 如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点.有一点P在C,D之间运动(不与C,D两点重合),在它运动的过程中,∠1+∠3=∠2这一相等关系是否始终成立?试说明理由.
如图,直线l1∥l2,直线l3与直线l1,l2分别交于C,D两点.有一点P在C,D之间运动(不与C,D两点重合),在它运动的过程中,∠1+∠3=∠2这一相等关系是否始终成立?试说明理由. 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,求证:四边形ABCD是正方形.
如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,求证:四边形ABCD是正方形.