题目内容
如图,AB为⊙O的直径,点C为圆上一定点,AC=6,BC=8,P为⊙O上一动点,过C作CQ⊥CP,交PB延长线于Q.
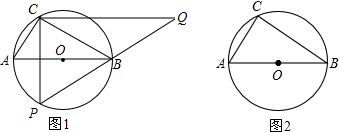
(1)若P点与C点关于AB对称,如图1,求CP的长;
(2)当P点运动到何处时,△PCQ的内心在线段CB上,请利用图2说明理由并求出此时四边形APBC的面积.

(1)若P点与C点关于AB对称,如图1,求CP的长;
(2)当P点运动到何处时,△PCQ的内心在线段CB上,请利用图2说明理由并求出此时四边形APBC的面积.
考点:三角形的内切圆与内心
专题:计算题
分析:(1)如图1,根据圆周角定理由AB为⊙O的直径得到∠ACB=90°,则根据勾股定理可计算出AB=10,再利用对称的性质得CP⊥AB,CH=PH,然后根据面积法可计算出CH=
,则PC=2CH=
;
(2)若点P为半圆AB的中点,即
=
,根据圆周角定理得到∠ACP=∠BCP=∠BCP=45°,而∠PCQ=90°,则得到CB平分∠PCQ,于是根据内心的性质得△PCQ的内心在线段CB上;再证明△APB为等腰直角三角形得到PA=PB=
AB=5
,然后利用四边形APBC的面积=S△ABC+S△ABP进行计算即可.
| 24 |
| 5 |
| 48 |
| 5 |
(2)若点P为半圆AB的中点,即
 |
| PA |
 |
| PB |
| ||
| 2 |
| 2 |
解答:解:(1)如图1,
∵AB为⊙O的直径,
∴∠ACB=90°,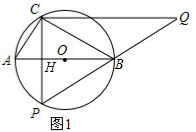
在Rt△ACB中,∵AC=6,BC=8,
∴AB=
=10,
∵P点与C点关于AB对称,
∴CP⊥AB,CH=PH,
∵
CH•AB=
AC•BC,
∴CH=
=
,
∴PC=2CH=
;
(2)当P点运动到半圆AB的中点时,△PCQ的内心在线段CB上,如图2,
∵点P为半圆AB的中点,
∴
=
,
∴∠ACP=∠BCP,
而∠ACB=90°,
∴∠BCP=45°,
∵CQ⊥CP,
∴∠PCQ=90°,
∴CB平分∠PCQ,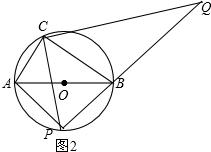
∴△PCQ的内心在线段CB上;
∵∠PAB=∠BCP=45°,∠PBA=∠ACP=45°,
∴△APB为等腰直角三角形,
∴PA=PB=
AB=5
,
∴四边形APBC的面积=S△ABC+S△ABP
=
•6•8+
•5
•5
=49.
∵AB为⊙O的直径,
∴∠ACB=90°,

在Rt△ACB中,∵AC=6,BC=8,
∴AB=
| AC2+BC2 |
∵P点与C点关于AB对称,
∴CP⊥AB,CH=PH,
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CH=
| 6×8 |
| 10 |
| 24 |
| 5 |
∴PC=2CH=
| 48 |
| 5 |
(2)当P点运动到半圆AB的中点时,△PCQ的内心在线段CB上,如图2,
∵点P为半圆AB的中点,
∴
 |
| PA |
 |
| PB |
∴∠ACP=∠BCP,
而∠ACB=90°,
∴∠BCP=45°,
∵CQ⊥CP,
∴∠PCQ=90°,
∴CB平分∠PCQ,

∴△PCQ的内心在线段CB上;
∵∠PAB=∠BCP=45°,∠PBA=∠ACP=45°,
∴△APB为等腰直角三角形,
∴PA=PB=
| ||
| 2 |
| 2 |
∴四边形APBC的面积=S△ABC+S△ABP
=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
=49.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了圆周角定理和勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 【探索研究】我们可借鉴以前研究函数的经验,探索函数y=x+
【探索研究】我们可借鉴以前研究函数的经验,探索函数y=x+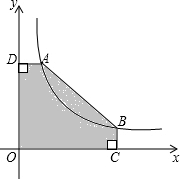 如图,A(2,m),B(6,n)是双曲线y=
如图,A(2,m),B(6,n)是双曲线y=