题目内容
 如图,在△ABC中,点O是边AC上的一个动点,过O点作直线MN∥BC,设MN交∠ACB的角平分线于点E,交∠ACB外角的平分线于点F.
如图,在△ABC中,点O是边AC上的一个动点,过O点作直线MN∥BC,设MN交∠ACB的角平分线于点E,交∠ACB外角的平分线于点F.(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
(3)若∠BAC=45°,四边形AECF是正方形,求AO:BC的值.
考点:矩形的判定,等腰三角形的判定与性质,正方形的判定
专题:
分析:(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案;
(2)根据平行四边形的判定以及矩形的判定得出即可;
(3)利用正方形的对角线相互垂直平分且相等的性质、等腰直角三角形的判定与性质进行解答.
(2)根据平行四边形的判定以及矩形的判定得出即可;
(3)利用正方形的对角线相互垂直平分且相等的性质、等腰直角三角形的判定与性质进行解答.
解答:(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.

(3)∵四边形AECF是正方形,
∴AC⊥EF,AC=EF,且AO=
AC,
又∵∠BAC=45°,
∴∠B=∠BAC=45°,
∴BC=AC.
∴AO:BC=AO:AC=1:2.
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.

(3)∵四边形AECF是正方形,
∴AC⊥EF,AC=EF,且AO=
| 1 |
| 2 |
又∵∠BAC=45°,
∴∠B=∠BAC=45°,
∴BC=AC.
∴AO:BC=AO:AC=1:2.
点评:此题主要考查了矩形的判定、平行四边形的判定和直角三角形的判定等知识,根据已知得出∠ECF=90°是解题关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
下列由左边到右边的变形中,是因式分解的是( )
| A、(x+2)(x-2)=x2-4 | ||
| B、x2-4=(x+2)(x-2) | ||
| C、x2-4+3x=(x+2)(x-2)+3x | ||
D、x2-1=x(x-
|
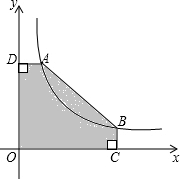 如图,A(2,m),B(6,n)是双曲线y=
如图,A(2,m),B(6,n)是双曲线y=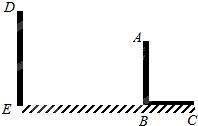 已知,如图,AB和DE是直立在地面上的两根立柱AB=6m,某一时刻AB在太阳光下的投影BC=3m.
已知,如图,AB和DE是直立在地面上的两根立柱AB=6m,某一时刻AB在太阳光下的投影BC=3m. 如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,且DE∥AB,求证:△ABC≌△DEF.
如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,且DE∥AB,求证:△ABC≌△DEF.