题目内容

11．若a1，a2，a3，…，a2014，a2015均为正数，M=（a1+a2+…+a2014）•（a2+a3+…+a2015），又N=（a1+a2+…+a2015）•（a2+a3+…+a2014），则M与N的大小关系是（　　）
A．M=NB．M＜NC．M＞ND．无法比较

分析 先求出M-N的值，再根据求出的结果比较即可．

解答 解：∵a1，a2，a3，…，a2014，a2015均为正数，M=（a1+a2+…+a2014）•（a2+a3+…+a2015），又N=（a1+a2+…+a2015）•（a2+a3+…+a2014），
∴M-N=（a1+a2+…+a2014）•（a2+a3+…+a2015）-（a1+a2+…+a2015）•（a2+a3+…+a2014）
=（a1+a2+…+a2014）•（a2+a3+…+a2014+a2015）-（a1+a2+…+a2014+a2015）•（a2+a3+…+a2014）
=（a1+a2+…+a2014）•（a2+a3+…+a2014）+（a1+a2+…+a2014）•a2015-（a1+a2+…+a2014）•（a2+a3+…+a2014）-a2015•（a2+a3+…+a2014）
=a1•a2015＞0，
则M与N的大小关系是M＞N，
故选C．

点评 本题考查了整式的混合运算，能选择适当的方法比较两个数的大小是解此题的关键．

练习册系列答案
相关题目
13．如图，已知∠AOB=α，∠BOC=β，OM平分∠AOC，ON平分∠BOC，则∠MON的度数是（　　）
A．$\frac{1}{2}$βB．$\frac{1}{2}$（α-β）C．α-$\frac{1}{2}$βD．$\frac{1}{2}$α
14．下列图形中不是轴对称图形的是（　　）
A．B．C．D．
11．在平面直角坐标系xOy中，y轴上有一点P，它到点A（4，3），B（3，-1）的距离之和最小，则点P的坐标是（　　）
A．（0，0）B．（0，$\frac{4}{7}$）C．（0，$\frac{5}{7}$）D．（0，$\frac{4}{5}$）
6．如图，在△ABC中，AD平分∠BAC，CD⊥AD于点D，∠DCB=∠B．若AC=10，AB=25，求CD的长．
16．如图，线段AB、CD互相平分交于点O，则下列结论错误的是（　　）
A．AD=BCB．∠C=∠DC．AD∥BCD．OC=OB
3．如图所示，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．
（1）证明：不论E、F在BC、CD上如何滑动，总有BE=CF；
（2）当点E、F在BC、CD上滑动时，探讨四边形AECF的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大（或最小）值．
20．（1）如图（1），BD平分∠ABC，DE∥BC，且AE=BE，求证：AB=BC；
（2）如图（2），∠1=∠2，∠3=∠4，EF过点O，且EF∥BC，求证：EF=BE+CF；
（3）如图（3），∠1=∠2，∠3=∠4，EF过点O，且EF∥BC，求证：EF=BE-CF．
1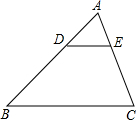．如图，在△ABC中，DE∥BC，若AD：DB=1：3，DE=4，则BC=（　　）
A．10B．12C．15D．16

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网