题目内容
6. 如图,在△ABC中,AD平分∠BAC,CD⊥AD于点D,∠DCB=∠B.若AC=10,AB=25,求CD的长.
如图,在△ABC中,AD平分∠BAC,CD⊥AD于点D,∠DCB=∠B.若AC=10,AB=25,求CD的长.
分析 如图,延长CD交AB于点E,构建全等三角形:△ADE≌△ADC(ASA).由全等三角形的对应边相等推知AE=AC=10,DE=DC;根据BE=CE,AB=25,得出AB=AE+BE=10+2DC=25,即可求得DC=7.5.
解答  解:如图,延长CD交AB于点E.
解:如图,延长CD交AB于点E.
∵AD平分∠BAC,
∴∠1=∠2.
∵CD⊥AD,
∴∠ADE=∠ADC=90°.
∵在△ADE与△ADC中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AD=AD}\\{∠ADE=∠ADC}\end{array}\right.$,
∴△ADE≌△ADC(ASA).
∴AE=AC=10,DE=DC.
∵∠DCB=∠B,
∴BE=CE=2DC.
∴AB=AE+BE=10+2DC=25.
∴DC=7.5.
点评 本题考查了全等三角形的判定与性质、等腰三角形的性质.注意此题中辅助线的作法.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
8.在-3.1415926,$\sqrt{10}$,$\frac{22}{7}$,9π,$\frac{\sqrt{5}}{5}$,$\root{3}{8}$中,无理数有( )个.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
9.据报道,2014年宁波全市口岸进出口总额为2186.1亿美元,将2186.1亿用科学记数法表示为( )
| A. | 2.1861×108 | B. | 2.1861×109 | C. | 2.1861×1010 | D. | 2.1861×1011 |
6.世界数学史上首次正式引入负数是在中国古代数学著作《九章算术》里,若收入100元记作+100元,则-80元表示( )
| A. | 支出20元 | B. | 收入20元 | C. | 支出80元 | D. | 收入80元 |
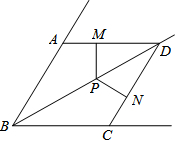 如图,已知在∠ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:
如图,已知在∠ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证: 如图所示,已知△ABC中,∠C=90°,AB=5cm,AC=3cm,BC=4cm,AD是∠CAB的平分线,与BC交于D,DE⊥AB于E,则
如图所示,已知△ABC中,∠C=90°,AB=5cm,AC=3cm,BC=4cm,AD是∠CAB的平分线,与BC交于D,DE⊥AB于E,则