Question

14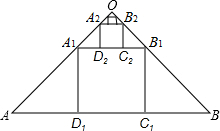．如图，在斜边长为1的等腰直角三角形OAB中，作内接正方形A₁B₁C₁D₁；在等腰直角三角形OA₁B₁中作内接正方形A₂B₂C₂D₂；在等腰直角三角形OA₂B₂中作内接正方形A₃B₃C₃D₃；…；依次作下去，则第2016个正方形A₂₀₁₆B₂₀₁₆C₂₀₁₆D₂₀₁₆的边长是$（\frac{1}{3}）^{2016}$．

Answer 1

分析 根据等腰直角三角形和正方形的性质可以得出A_nD_n+1=D_n+1C_n+1=C_n+1B_n=$\frac{1}{3}$A_nB_n，再结合AB=1即可得出A_nB_n=$（\frac{1}{3}）^{n}$，代入n=2016即可得出结论．

解答 解：∵△OA_nB_n为等腰直角三角形，
∴A_nD_n+1=D_n+1C_n+1=C_n+1B_n=$\frac{1}{3}$A_nB_n，
∵AB=1，
∴A_nB_n=$（\frac{1}{3}）^{n}$，
∴第2016个正方形A₂₀₁₆B₂₀₁₆C₂₀₁₆D₂₀₁₆的边长是$（\frac{1}{3}）^{2016}$．
故答案为：$（\frac{1}{3}）^{2016}$．

点评 本题考查了正方形的性质以及等腰直角三角形的性质，解题的关键是找出A_nB_n=$（\frac{1}{3}）^{n}$．本题属于基础题，难度不大，解决该题型题目时，根据正方形和等腰直角三角形的性质找出正方形的边长通式是关键．