题目内容
12.下列各组里的二次根式是不是同类二次根式?(1)$\sqrt{63}$,$\sqrt{28}$;
(2)$\sqrt{12}$,$\sqrt{27}$,4$\sqrt{\frac{1}{3}}$;
(3)$\sqrt{4{x}^{3}}$,2$\sqrt{2x}$;
(4)$\sqrt{18}$,$\sqrt{50}$,2$\sqrt{\frac{2}{9}}$;
(5)$\sqrt{2x}$,$\sqrt{2{a}^{2}{x}^{3}}$,$\sqrt{50x{y}^{2}}$.
分析 分别将被开方数分解质因数,根据$\sqrt{{a}^{2}}$=a(a>0)化简,被开方数是分数的利用$\sqrt{\frac{b}{a}}$=$\frac{\sqrt{b}}{\sqrt{a}}$(b≥0,a>0)进行化简;化成最简二次根式后被开方数相同的二次根式是同类二次根式.
解答 解:(1)$\sqrt{63}$=$\sqrt{7×9}$=3$\sqrt{7}$,$\sqrt{28}$=$\sqrt{4×7}$=2$\sqrt{7}$,
所以$\sqrt{63}$、$\sqrt{28}$是同类二次根式;
(2)$\sqrt{12}$=$\sqrt{3×4}$=2$\sqrt{3}$,$\sqrt{27}$=$\sqrt{3×9}$=3$\sqrt{3}$,4$\sqrt{\frac{1}{3}}$=4×$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
所以$\sqrt{12}$、$\sqrt{27}$、4$\sqrt{\frac{1}{3}}$是同类二次根式;
(3)$\sqrt{4{x}^{3}}$=2x$\sqrt{x}$,2$\sqrt{2x}$,
所以$\sqrt{4{x}^{3}}$、2$\sqrt{2x}$不是同类二次根式;
(4)$\sqrt{18}$=$\sqrt{2×9}$=3$\sqrt{2}$,$\sqrt{50}$=$\sqrt{2×25}$=5$\sqrt{2}$,2$\sqrt{\frac{2}{9}}$=2×$\frac{\sqrt{2}}{3}$=$\frac{2\sqrt{2}}{3}$,
所以$\sqrt{18}$、$\sqrt{50}$、2$\sqrt{\frac{2}{9}}$是同类二次根式;
(5)$\sqrt{2x}$,$\sqrt{2{a}^{2}{x}^{3}}$=ax$\sqrt{2x}$,$\sqrt{50x{y}^{2}}$=5y$\sqrt{2x}$,
所以$\sqrt{2x}$、$\sqrt{2{a}^{2}{x}^{3}}$、$\sqrt{50x{y}^{2}}$是同类二次根式.
点评 本题考查了同类二次根式的判别,首先要熟练掌握二次根式的化简,能正确将二次根式化成最简二次根式,最简二次根式的条件是:(1)被开方数的因数是整数或字母,因式是整式;(2)被开方数中不含有可化为平方数或平方式的因数或因式;然后根据同类二次根式的定义进行判别.

 阅读快车系列答案
阅读快车系列答案| A. | -51 | B. | -52 | C. | -53 | D. | -54 |
| 数量x(千克) | 1 | 2 | 3 | 4 |
| 售价y(元) | 2+0.1 | 4+0.2 | 6+0.3 | 8+0.4 |
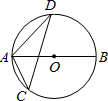 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=52°,则∠BAD=38°.
如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=52°,则∠BAD=38°. 如图,抛物线y=x2+bx经过原点O,与x轴相交于点A(1,0),
如图,抛物线y=x2+bx经过原点O,与x轴相交于点A(1,0),