Question

5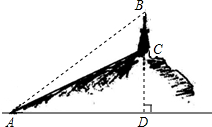．如图，要测量小山上电视塔BC的高度，在山脚下点A测得：塔顶B的仰角为∠BAD=40°，塔底C的仰角为∠CAD=30°，AC=200米，求电视塔BC的高．（结果用含非特殊角的锐角三角函数及根式表示即可）

Answer 1

分析 要求BC的长，由题意知可先求出BD、CD的长．再利用BC=BD-CD求出BC的长．

解答 解：在Rt△ADC中，∠ADC=90°，∠CAD=30°，AC=200米．
∴CD=100米，
∴AD=AC•cos∠CAD=200×$\frac{\sqrt{3}}{2}$=100$\sqrt{3}$，
在Rt△ADB中，∠ADB=90°，∠BAD=40°，AD=100$\sqrt{3}$，
∴BD=AD•tan∠BAD=100$\sqrt{3}$tan40°，
∴BC=BD-CD=100$\sqrt{3}$tan40°-100（米）．

点评 本题考查了解直角三角形的应用，解题的关键是掌握构造仰角所在的直角三角形，利用两个直角三角形的公共边求解是常用的解直角三角形的方法．