题目内容
九年级数学兴趣小组组织了以“等积变形”为主题的课题研究.
第一学习小组发现:如图(1),点A、点B在直线l1上,点C、点D在直线l2上,若l1∥l2,则S△ABC=S△ABD;反之亦成立.
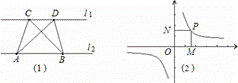

第二学习小组发现:如图(2),点P是反比例函数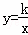 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
请利用上述结论解决下列问题:
(1)如图(3),四边形ABCD、与四边形CEFG都是正方形点E在CD上,正方形ABCD边长为2,则 =
=
_________.
(2)如图(4),点P、Q在反比例函数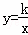 图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若
图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若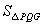 =8,则
=8,则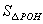 =_________,k=_________.
=_________,k=_________.
(3)如图(5)点P、Q是第一象限的点,且在反比例函数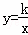 图象上,过点P作x轴垂线,过点Q作y轴
图象上,过点P作x轴垂线,过点Q作y轴
垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
(1)2;(2)2、-4;(3)PQ∥MN
【解析】(1)根据组合图形的面积求法得出三角的面积;(2)根据反比例的性质以及三角形的面积的求法进行求法;(3)作PA⊥y轴,QB⊥x轴,垂足为A,B,连接PN,MQ,根据双曲线的性质进行计算.
(1)2 (2)2, k=﹣4
(3)PQ∥MN.
理由:作PA⊥y轴,QB⊥x轴,垂足为A,B,连接PN,MQ,根据双曲线的性质可知,S矩形AOMP=S矩形BONQ=k,∴S矩形ANCP=S矩形BMCQ,可知S△NCP=S△MCQ, ∴S△NPQ=S△MPQ, ∴PQ∥MN.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 某市的水果加工厂P恰好在两条铁路OA、OB的夹角内部,为了抓住这个千载难逢的机遇,提高水果的销量,经理决定在这两条铁路沿线上各建一个运转站M、N,把加工厂的水果每天从加工厂P运往M、N请问M、N应建在何处,能够使P、M、N之间运转的路程最短.
某市的水果加工厂P恰好在两条铁路OA、OB的夹角内部,为了抓住这个千载难逢的机遇,提高水果的销量,经理决定在这两条铁路沿线上各建一个运转站M、N,把加工厂的水果每天从加工厂P运往M、N请问M、N应建在何处,能够使P、M、N之间运转的路程最短. 的值.
的值.

 =1s时,S的值是多少?
=1s时,S的值是多少? 时,点E、F、G分别在边AB、BC、CD上移动,用含t的代数式表示S;当
时,点E、F、G分别在边AB、BC、CD上移动,用含t的代数式表示S;当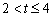 时,点E在边AB上移动,点F、G都在边CD上移动,用含t的代数式表示S.
时,点E在边AB上移动,点F、G都在边CD上移动,用含t的代数式表示S. 点的三角形相似?请说明理由
点的三角形相似?请说明理由
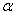 (
(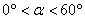 ),将线段BC绕点B逆时针旋转60°得到线段BD.
),将线段BC绕点B逆时针旋转60°得到线段BD.