题目内容
11.在二次根式$\sqrt{48},\sqrt{3{m^2}},\sqrt{11},\sqrt{5a},\sqrt{{x^2}+1},\sqrt{{a^2}-2ab+{b^2}},\sqrt{\frac{x}{9}}$中,最简二次根式有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解答 解:$\sqrt{48}$=$\sqrt{{4}^{2}×3}$,被开方数中含有能开得尽方的因数42,不是最简二次根式;
$\sqrt{3{m}^{2}}$,被开方数中含有能开得尽方的因式m2,不是最简二次根式;
$\sqrt{{a}^{2}-2ab+{b}^{2}}$=$\sqrt{(a-b)^{2}}$,被开方数中含有能开得尽方的因式(a-b)2,不是最简二次根式;
$\sqrt{11}$,$\sqrt{5a}$,$\sqrt{{x}^{2}+1}$符合最简二次根式的定义.
故选:C.
点评 本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或因式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.对于方程:3x+2y=4,下列说法正确的是( )
| A. | 无正数解 | B. | 只有一组正数解 | ||
| C. | 无正整数解 | D. | 只有一组正整数解 |
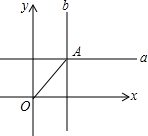 如图,在平面直角坐标系xOy中,分别平行x、y轴的两直线a、b相交于点A(3,4).连接OA,
如图,在平面直角坐标系xOy中,分别平行x、y轴的两直线a、b相交于点A(3,4).连接OA,