题目内容
14．
已知：在△ABC中，AB=AC．（1）尺规作图：作AD⊥BC于点D．（不要求写作法，保留作图痕迹）
（2）延长AD至E点，使得DE=AD．求证：四边形ABEC是菱形．
分析 （1）利用过直线外一点作直线的作法得出符合题意的图形即可；
（2）利用菱形的判定方法：对角线互相垂直且互相平分的四边形是菱形进而求出即可．
解答 解：（1）如图所示：
；
（2）证明：如图所示：
∵AB=AC，AD⊥BC，
∴CD=BD，
∵AD=DE，
∴四边形ABEC是平行四边形，
又∵AD⊥BC，
∴四边形ABEC是菱形．
点评 此题主要考查了基本作图以及菱形的判定方法，正确掌握菱形的判定方法是解题关键．
练习册系列答案
考前必练系列答案
相关题目
5．已知实数x，y满足（x-1）2+|y+3|=0，则x+y的值为（ ）
| A． | 4 | B． | 2 | C． | -2 | D． | -4 |
2．对于任意实数a、b，定义f（a，b）=a2+5a-b，如：f（2，3）=22+5×2-3，若f（x，2）=4，则实数x的值是（ ）
| A． | 1或-6 | B． | -1或6 | C． | -5或1 | D． | 5或-1 |
9．如图图形既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
6．某蒜苔生产基地收获蒜苔200吨．计划采用批发、零售、冷库储藏后销售三种方式出售，计划平均每吨的售价及成本如表：
经过一段时间，蒜苔按计划全部售出获得的总利润为y（元），蒜苔零售x（吨），且零售量是批发量的$\frac{1}{3}$．
（l）求y与x之间的函数关系式；
（2）由于受条件限制，经冷库储藏售出的蒜苔最多80吨，求该生产基地全部售完蒜苔获得的最大利润．
| 销售方式 | 批发 | 零售 | 储藏后销售 |
| 售价（元/吨） | 3000 | 4500 | 5500 |
| 成本（元/吨） | 700 | 1000 | 1200 |
（l）求y与x之间的函数关系式；
（2）由于受条件限制，经冷库储藏售出的蒜苔最多80吨，求该生产基地全部售完蒜苔获得的最大利润．
3．厦门市2014年中考体育考试中，某校九年级（3）班50人参加考试，具体的成绩与人数如表，则该班的中考体育的平均成绩是23.6分．
| 成绩 | 人数 |
| 25 | 24 |
| 24 | 10 |
| 22 | 10 |
| 20 | 6 |
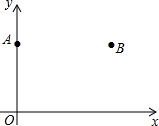如图，在平面直角坐标系xOy中，点A（0，3），点B（4，3）．