题目内容
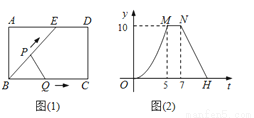
如图(1),E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,运动的速度都是1cm/秒.设P、Q同发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②cos∠ABE=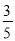 ;③当0<t≤5时,y=
;③当0<t≤5时,y=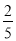 t2;④当t=
t2;④当t=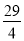 秒时,△ABE∽△QBP;其中正确的结论是______(填序号).
秒时,△ABE∽△QBP;其中正确的结论是______(填序号).
练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目

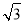 7.(填“>”、“=”、“<”)
7.(填“>”、“=”、“<”)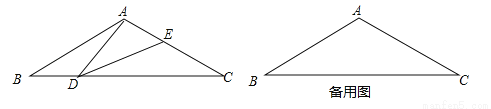
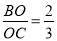 ,AD=10,则AO=______.
,AD=10,则AO=______.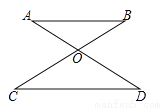
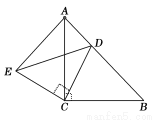
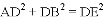 .
.
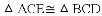
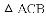
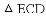
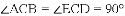
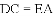
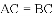

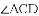

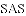
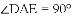
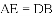
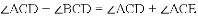
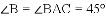
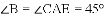
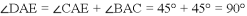
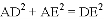 .
.