题目内容
(1)在一个边长为(10| 15 |
| 5 |
| 15 |
| 5 |
(2)借助计算器可以求得
| 42+32 |
| 442+332 |
| 4442+3332 |
| 44442+33332 |
|
分析:(1)中,根据正方形的面积公式列式计算,计算的时候注意运用平方差公式简便计算;
(2)中,首先计算特例的值,再观察找规律,进而推广到一般.
(2)中,首先计算特例的值,再观察找规律,进而推广到一般.
解答:解:(1)(10
+5
)2-(10
-5
)2
=(10
+5
+10
-5
)(10
+5
-10
+5
))
=20
×10
=1000
;
(2)∵
=
=5,
=55,…
故前面有多少个4,后面就有多少个5.
∴原式=
.
| 15 |
| 5 |
| 15 |
| 5 |
=(10
| 15 |
| 5 |
| 15 |
| 5 |
| 15 |
| 5 |
| 15 |
| 5 |
=20
| 15 |
| 5 |
=1000
| 3 |
(2)∵
| 42+32 |
| 25 |
| 442+332 |
故前面有多少个4,后面就有多少个5.
∴原式=
| ||
| 2005个 |
点评:(1)中,特别注意计算的时候运用平方差公式较为简便;
(2)中,首先由特例找规律,再得结论.
(2)中,首先由特例找规律,再得结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
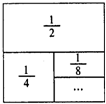 如图,在一个边长为1的正方形纸板上,依次贴上面积为
如图,在一个边长为1的正方形纸板上,依次贴上面积为 23、如图所示在一个边长为a的正方形木板上,锯掉边长为b的四个小正方形,计算当a=18分米,b=6分米时剩余部分的面积.
23、如图所示在一个边长为a的正方形木板上,锯掉边长为b的四个小正方形,计算当a=18分米,b=6分米时剩余部分的面积. 如图所示,在一个边长为2cm的正方形纸片中,剪去一个边长为2cm的等边三角形,求出图中阴影部分的面积.(取
如图所示,在一个边长为2cm的正方形纸片中,剪去一个边长为2cm的等边三角形,求出图中阴影部分的面积.(取