题目内容
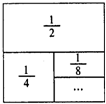 如图,在一个边长为1的正方形纸板上,依次贴上面积为
如图,在一个边长为1的正方形纸板上,依次贴上面积为| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
分析:由题意可知正方形的总面积为1,然后,通过观察未贴部分,来确定已贴部分总面积:贴
,余
;再贴
,余
,则
+
=1-
=
;再贴
,余
,则
+
+
=1-
=
,所以,
+
+…+
=1-
=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 7 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
| 1 |
| 2n |
| 2n-1 |
| 2n |
解答:解:∵正方形的边长为1,
∴正方形的面积为1,
∵正方形减去未贴部分的面积既是已帖部分的面积,
∴
+
=1-
=
=
,
∴
+
+
=1-
=
=
,
∴
+
+…+
=1-
=
.
故答案为
.
∴正方形的面积为1,
∵正方形减去未贴部分的面积既是已帖部分的面积,
∴
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 22-1 |
| 22 |
∴
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 7 |
| 8 |
| 23-1 |
| 23 |
∴
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
| 1 |
| 2n |
| 2n-1 |
| 2n |
故答案为
| 2n-1 |
| 2n |
点评:本题主要考查通过分析总结归纳规律,关键在于用“数形结合”的思想,分析出余下部分的面积,即可推出已帖部分的面积.

练习册系列答案
相关题目
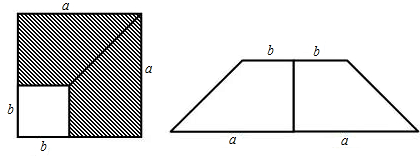
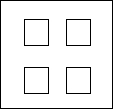 如图,在一个边长为acm的正方形木板上,挖掉四个边长为bcm(
如图,在一个边长为acm的正方形木板上,挖掉四个边长为bcm(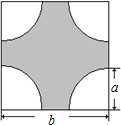 如图,在一个边长为b厘米的正方形铁板的四角,各剪去一个半径为a厘米(a
如图,在一个边长为b厘米的正方形铁板的四角,各剪去一个半径为a厘米(a 我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”如图,在一个边长为1的正方形纸版上,依次贴上面积为
我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”如图,在一个边长为1的正方形纸版上,依次贴上面积为