题目内容
 如图所示,在一个边长为2cm的正方形纸片中,剪去一个边长为2cm的等边三角形,求出图中阴影部分的面积.(取
如图所示,在一个边长为2cm的正方形纸片中,剪去一个边长为2cm的等边三角形,求出图中阴影部分的面积.(取| 3 |
分析:过点E作EF⊥BC于点F,根据锐角三角函数的定义求出EF的长,由S阴影=S正方形ABCD-S△BCE即可得出结论.
解答: 解:过点E作EF⊥BC于点F,
解:过点E作EF⊥BC于点F,
∵△BEC是边长为2的等边三角形,
∴EF=BE•sin60°=2×
=
,
∴S阴影=S正方形ABCD-S△BCE
=2×2-
×2×
=4-
≈4-1.73
=2.27.
 解:过点E作EF⊥BC于点F,
解:过点E作EF⊥BC于点F,∵△BEC是边长为2的等边三角形,
∴EF=BE•sin60°=2×
| ||
| 2 |
| 3 |
∴S阴影=S正方形ABCD-S△BCE
=2×2-
| 1 |
| 2 |
| 3 |
=4-
| 3 |
≈4-1.73
=2.27.
点评:本题考查的是正方形的性质,熟知正方形的四条边都相等,四个角都是直角是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
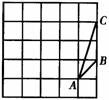
 如图所示,在由边长为1的25个小正方形组成的正方形网格上有一个△ABC,试在这个网格上画一个与△ABC相似,且面积最大的△A1B1C1(A1,B1,C1三点都在格点上),并求出这个三角形的面积.
如图所示,在由边长为1的25个小正方形组成的正方形网格上有一个△ABC,试在这个网格上画一个与△ABC相似,且面积最大的△A1B1C1(A1,B1,C1三点都在格点上),并求出这个三角形的面积.
 ,
, ,
, ,…,
,…, 的矩形彩色纸片(n为大于1的整数).请你用,依数形变化的规律,计算:
的矩形彩色纸片(n为大于1的整数).请你用,依数形变化的规律,计算: ________.
________.