题目内容
7.先化简,再求值:$\frac{{a}^{2}-{b}^{2}}{b}$÷($\frac{{a}^{2}-2ab}{b}$+b),其中a=2sin60°+tan45°,b=tan60°-2cos60°.分析 首先化简$\frac{{a}^{2}-{b}^{2}}{b}$÷($\frac{{a}^{2}-2ab}{b}$+b),然后把a=2sin60°+tan45°,b=tan60°-2cos60°代入化简后的算式,求出算式的值是多少即可.
解答 解:$\frac{{a}^{2}-{b}^{2}}{b}$÷($\frac{{a}^{2}-2ab}{b}$+b)
=$\frac{{a}^{2}-{b}^{2}}{b}$÷$\frac{{(a-b)}^{2}}{b}$
=$\frac{a+b}{a-b}$
当a=2sin60°+tan45°,b=tan60°-2cos60°时,
原式=$\frac{2sin60°+tan45°+tan60°-2cos60°}{2sin60°+tan45°-tan60°+2cos60°}$
=$\frac{2\sqrt{3}}{2}$
=$\sqrt{3}$
点评 此题主要考查了分式的化简求值问题,要熟练掌握,化简求值,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
2.以下列各组线段为边,能组成三角形的是( )
| A. | 2,2,4 | B. | 2,3,6 | C. | 1,2,3 | D. | 3,4,5 |
16.某超市销售进价为2元的雪糕,在销售中发现,此商品的日销售单价x(元)与日销售量y(根)之间有如下关系:
(1)猜测并确定y和x之间的函数关系式;
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由.
| 日销售单价x(元) | 3 | 4 | 5 | 6 |
| 日销售量y(根) | 40 | 30 | 24 | 20 |
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由.
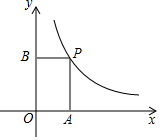 已知如图,在平面直角坐标系中,点P是反比例函数y=$\frac{{k}^{2}}{x}$(x>0)的图象上的一点,分别过P作PA⊥x轴于点A,PB⊥y轴于点B,若四边形OAPB的面积为4,则k值为( )
已知如图,在平面直角坐标系中,点P是反比例函数y=$\frac{{k}^{2}}{x}$(x>0)的图象上的一点,分别过P作PA⊥x轴于点A,PB⊥y轴于点B,若四边形OAPB的面积为4,则k值为( )