题目内容
5.解不等式组$\left\{\begin{array}{l}{-2x≤6①}\\{3(x+1)<2x+5②}\end{array}\right.$请结合题意填空,完成本题的解答.(Ⅰ)解不等式①,得x≥-3;
(Ⅱ)解不等式②,得x<2;
(Ⅲ)把不等式①和②的阶级在数轴上表示出来;
(Ⅳ)原不等式组的解集为-3≤x<2
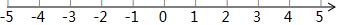
分析 (Ⅰ)系数化成1即可求解;
(Ⅱ)去括号、移项、合并同类项、系数化成1即可求解;
(Ⅲ)把(1)和(2)求得解集在数轴上表示出来即可;
(Ⅳ)两个解集的公共部分就是不等式组的解集.
解答 解:(Ⅰ)系数化成1得x≥-3.
故答案是:x≥-3;
(Ⅱ)去括号,得3x+3<2x+5,
移项,得3x-2x<5-3,
合并同类项,得x<2.
故答案是:x<2;
(Ⅲ) ;
;
(Ⅳ)不等式组的解集是-3≤x<2.
故答案是:-3≤x<2.
点评 本题考查了解一元一次不等式组:求不等式组的解集的过程叫解不等式组.解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
16.某超市销售进价为2元的雪糕,在销售中发现,此商品的日销售单价x(元)与日销售量y(根)之间有如下关系:
(1)猜测并确定y和x之间的函数关系式;
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由.
| 日销售单价x(元) | 3 | 4 | 5 | 6 |
| 日销售量y(根) | 40 | 30 | 24 | 20 |
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由.

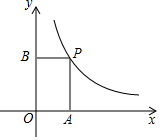 已知如图,在平面直角坐标系中,点P是反比例函数y=$\frac{{k}^{2}}{x}$(x>0)的图象上的一点,分别过P作PA⊥x轴于点A,PB⊥y轴于点B,若四边形OAPB的面积为4,则k值为( )
已知如图,在平面直角坐标系中,点P是反比例函数y=$\frac{{k}^{2}}{x}$(x>0)的图象上的一点,分别过P作PA⊥x轴于点A,PB⊥y轴于点B,若四边形OAPB的面积为4,则k值为( )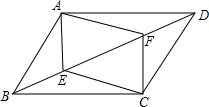 如图,E、F是平行四边形ABCD对角线BD上的两点,且BE=DF.求证:四边形AECF是平行四边形.
如图,E、F是平行四边形ABCD对角线BD上的两点,且BE=DF.求证:四边形AECF是平行四边形.