题目内容
6.已知关于x的方程(m-1)x2-2mx+m+1=0.(1)此方程有实数根吗?请说明理由;
(2)若此方程有两个实数根,且两个根都为正整数,则整数m的值为?
分析 (1)根据根的判别式△=b2-4ac≥0解答即可;
(2)首先求出一元二次方程的两根,一根为1,一根为$1+\frac{2}{m-1}$,只需要求出$\frac{2}{m-1}$是正整数时m的值即可.
解答 解:(1)∵关于x的一元二次方程(m-1)x2-2mx+m+1=0有实数根,
∴m-1≠0,且△=b2-4ac=(-2m)2-4(m-1)•(m+1)=4≥0,
所以方程有实数根;
(2)∴x1=$\frac{2m-2}{2(m-1)}=1$,
x2=$\frac{2m+2}{2(m-1)}=\frac{m+1}{m-1}$,
x2=$\frac{m+1}{m-1}=1+\frac{2}{m-1}$,
∵方程的两个根都是正整数,
∴$\frac{2}{m-1}$是正整数,
∴m-1=1或2
∴m=2或3.
点评 本题主要考查了根的判别式的知识,解答本题的关键是掌握根的判别式与根的个数的关系,此题难度不大.

练习册系列答案
相关题目
11.A、B两家工厂生产同一型号的电池,现分别抽取了6节电池,测试连续使用时间,结果如表:
(1)计算两组数据的总和及平均数,并填表;
(2)哪家生产的电池质量更好一些?
| 项目 | 1 | 2 | 3 | 4 | 5 | 6 | 总和/h | 平均数/h |
| A厂家电池使用时间/h | 40 | 48 | 40 | 42 | 43 | 45 | ||
| B厂家电池使用时间/h | 40 | 50 | 45 | 46 | 46 | 52 |
(2)哪家生产的电池质量更好一些?
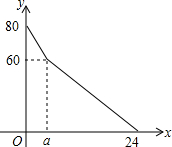 某超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待自助收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人.
某超市开设了自助收银区,实施自助收银,以节省顾客的排队时间.某日上午10点,超市值班经理发现在自助收银区已经有80人在等待自助收银,此时仍有顾客不断前来排队等候.在自助收银区,假设顾客按固定的速度增加,每个收银口自助收银的速度也是固定的,其中每分钟新增排队人数为3人,每分钟每个收银口自助收银2人. 如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,cosC=$\frac{\sqrt{2}}{2}$,sinB=$\frac{1}{3}$,AD=1.
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,cosC=$\frac{\sqrt{2}}{2}$,sinB=$\frac{1}{3}$,AD=1.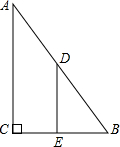 有一直角三角形的硬纸板,∠C=90°,BC=2,∠B=60°,沿中位线DE剪成两部分,将这两部分再拼成一个四边形,这个四边形的周长为3+3$\sqrt{3}$.
有一直角三角形的硬纸板,∠C=90°,BC=2,∠B=60°,沿中位线DE剪成两部分,将这两部分再拼成一个四边形,这个四边形的周长为3+3$\sqrt{3}$. “若x满足(80-x)(x-60)=30,求(80-x)2+(x-60)2的值”
“若x满足(80-x)(x-60)=30,求(80-x)2+(x-60)2的值”