题目内容
15.已知不等式组$\left\{\begin{array}{l}{x+2>m+n}\\{x-1<m-1}\end{array}\right.$的解集为-1<x<2,则(m+n)2017=1.分析 分别求出每个不等式的解集,根据该不等式组的解集为-1<x<2可得关于m、n的方程,解得m、n的值,代入计算可得.
解答 解:解不等式x+2>m+n,得:x>m+n-2,
解不等式x-1<m-1,得:x<m,
∵不等式组的解集为:-1<x<2,
∴m+n-2=-1,m=2,
解得:m=2,n=-1,
则(m+n)2017=(2-1)2017=1,
故答案为:1.
点评 本题考查的是解一元一次不等式组能力,将m、n看作常数求出每个不等式解集是前提和根本,结合其解集得到m、n的值是关键.

练习册系列答案
相关题目
7.某自行车厂计划平均每天生产200辆,但是由于种种原因,实际每天生产量与计划量相比有出入.表是某周的生产情况(超产记为正,减产记为负):
(1)根据记录的数据可知该厂星期三生产自行车多少辆?
(2)产量最多的一天比产量最少的一天多生产自行车多少辆?
(3)根据记录的数据可知该厂本周实际共生产自行车多少辆?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -3 | -7 | +14 | -10 | +16 | -4 |
(2)产量最多的一天比产量最少的一天多生产自行车多少辆?
(3)根据记录的数据可知该厂本周实际共生产自行车多少辆?
4.某校九年级(2)班学生参加体育考试,引体向上的成绩如表,该班级学生引体向上个数的众数与中位数分别是( )
| 引体向上的个数 | 7 | 8 | 9 | 10 | 11 |
| 人数 | 3 | 9 | 8 | 12 | 8 |
| A. | 9.5和10 | B. | 10和9.5 | C. | 9和10 | D. | 10和9 |
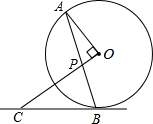 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
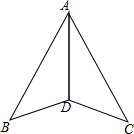 如图,∠ADB=∠ADC,AD平分∠BAC,你能证明△ABD≌△ACD吗?若BD=3cm,则CD有多长?
如图,∠ADB=∠ADC,AD平分∠BAC,你能证明△ABD≌△ACD吗?若BD=3cm,则CD有多长?